(本小题满分12分)如图1所示,在矩形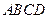 中,
中,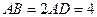 ,
, 为
为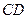 的中点,沿
的中点,沿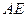 将
将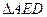 折起,如图2所示,在图2中,
折起,如图2所示,在图2中, 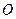 、
、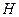 、
、 分别为
分别为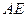 、
、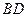 、
、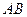 的中点,且
的中点,且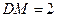 .
.
(Ⅰ)求证:  平面
平面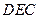 ;
;
(Ⅱ) 求证:面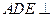 面
面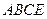 ;
;
(Ⅲ)求三棱锥 的体积.
的体积.
在 中,
中, 分别是角A,B,C对边,且
分别是角A,B,C对边,且 .
.
(I)若 求
求 的值
的值
(II)若 ,求
,求 面积的最大值
面积的最大值
(本小题满分10分)设圆满足:
(Ⅰ)截y轴所得弦长为2;
(Ⅱ)被x轴分成两段圆弧,其弧长的比为3∶1.
在满足条件(Ⅰ)、(Ⅱ)的所有圆中,求圆心到直线l:x-2y=0的距离最小的圆的方程.
(本小题满分10分)如图,在四棱锥S—ABCD中,侧棱SA=SB=SC=SD,底面ABCD是菱形,AC与BD交于O点.
(Ⅰ)求证:AC⊥平面SBD;
(Ⅱ)若E为BC中点,点P在侧面△SCD内及其边界上运动,并保持PE⊥AC,试指出动点P的轨迹,并证明你的结论.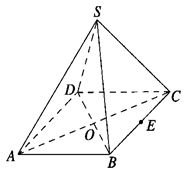
(本小题满分12分)如图,直三棱柱ABC—A1B1C1中,已知AC =BC = AA1=a,
∠ACB =90°,D 是A1B1中点.
(Ⅰ)求证:C1D ⊥平面A1B1BA ;
(Ⅱ)请问, 当点F 在BB1上什么位置时,会使得AB1⊥平面C1DF ?并证明你的结论.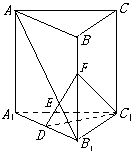
(本小题满分9分)已知圆C: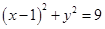 内有一点P(2,2),过点P作直线l交圆C于A、B两点.
内有一点P(2,2),过点P作直线l交圆C于A、B两点.
(Ⅰ)当l经过圆心C时,求直线l的方程;
(Ⅱ)当弦AB被点P平分时,写出直线l的方程;
(Ⅲ)当直线l的倾斜角为45º时,求弦AB的长.