(本小题满分12分) 月份,有一款新服装投入某市场销售,
月份,有一款新服装投入某市场销售, 月
月 日该款服装
日该款服装
仅销售出 件,
件, 月
月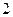 日售出
日售出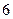 件,
件, 月
月 日售出
日售出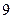 件,
件, 月
月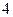 日售出
日售出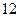 件,尔后,每天售
件,尔后,每天售
出的件数分别递增 件,直到日销售量达到最大(只有
件,直到日销售量达到最大(只有 天)后,每天销售的件数开始下降,
天)后,每天销售的件数开始下降,
分别递减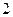 件,到
件,到 月
月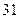 日刚好售出
日刚好售出 件.
件.
(Ⅰ)问 月几号该款
月几号该款 服装销售件数最多?其最大值是多少?
服装销售件数最多?其最大值是多少?
(Ⅱ)按规律,当该商场销售此服装达到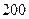 件时,社会上就开始流行,而日销售量连续下降
件时,社会上就开始流行,而日销售量连续下降
并低于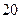 件时,则不再流行,问该款服装在社会上流行几天?说明理由.
件时,则不再流行,问该款服装在社会上流行几天?说明理由.
由下列各式: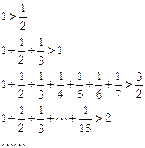
你能得出怎样的结论,并进行证明.
对于直线l:y=kx+1,是否存在这样的实数k,使得l与双曲线C:3x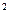 -y
-y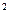 =1的交点A、B关于直线y=ax(a为常数)对称?若存在,求出k的值;若不存在,请说明理由。
=1的交点A、B关于直线y=ax(a为常数)对称?若存在,求出k的值;若不存在,请说明理由。
若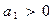 、
、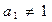 ,
,
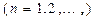
(1)求证: ;
;
(2)令 ,写出
,写出 、
、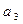 、
、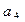 、
、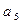 的值,观察并归纳出这个数列的通项公式
的值,观察并归纳出这个数列的通项公式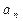 ;
;
(3)证明:存在不等于零的常数p,使 是等比数列,并求出公比q的值.
是等比数列,并求出公比q的值.
设虚数z1,z2,满足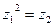 .
.
(1)若z1,z2又是一个实系数一元二次方程的两根,求z1, z2。
(2)若z1=1+mi(i为虚数单位,m∈R),  ,复数w=z2+3,求|w|的取值范围。
,复数w=z2+3,求|w|的取值范围。
求同时满足下列条件的所有复数z:(1) 是实数,且
是实数,且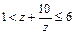 。
。
(2)z的实部和虚部都是整数。