(10分 )
)
问题提出
我们在分析解决某些数学问题时,经常要比较两个数或代数式的大小,而解决问题的策略一般要进行一定的转化,其中“作差法”就是常用的方法之一.所谓“作差法”:就是通过作差、变形,并利用差的符号确定他们的大小,即要比较代数式M、N的大小,只要作出它们的差M-N,若M-N>0,则M>N;若M-N=0,则M=N;若M-N<0,则M<N.
问题解决
如图1,把边长为a+b(a≠b)的大正方形分割成两个边长分别是a、b的小正方形及两个矩形,试比较两个小正方形面积之和M与两个矩形面积之和N的大小.
解:由图可知:M=a2+b2,N=2ab.
∴M-N=a2+b2-2ab=(a-b)2.
∵a≠b,∴(a-b)2>0.
∴M-N>0.
∴M>N.
类别应用
(1)已知小丽和小颖购买同一种商品的平均价格分别为 元/千克和
元/千克和 元/千克(a、b是正数,且a≠b),试比较小丽和小颖所购买商品的平均价格的高低.
元/千克(a、b是正数,且a≠b),试比较小丽和小颖所购买商品的平均价格的高低.
(2)试比较图2和图3中两个矩形周长M1、N1的大小(b>c).
联系拓广
小刚在超市里买了一些物品,用一个长方体的箱子“打包”,这个箱子的尺寸如图4所示(其中b>a>c>0),售货员分别可按图5、图6、图7三种方法进行捆绑,吻哪种方法用绳最短?哪种方法用绳最长?请说明理由.
如图,在 中, 为 的直径, 为 的弦,点 是 的中点,过点 作 的垂线,交 于点 ,交 于点 ,分别连接 , .
(1) 与 的数量关系是 ;
(2)求证: ;
(3)若 , ,求阴影部分图形的面积.

为庆祝"中国共产党的百年华诞",某校请广告公司为其制作"童心向党"文艺活动的展板、宣传册和横幅,其中制作宣传册的数量是展板数量的5倍,广告公司制作每件产品所需时间和利润如表:
|
产品 |
展板 |
宣传册 |
横幅 |
|
制作一件产品所需时间(小时) |
1 |
|
|
|
制作一件产品所获利润(元 |
20 |
3 |
10 |
(1)若制作三种产品共计需要25小时,所获利润为450元,求制作展板、宣传册和横幅的数量;
(2)若广告公司所获利润为700元,且三种产品均有制作,求制作三种产品总量的最小值.
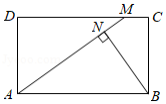
随着科学技术的不断进步,无人机被广泛应用到实际生活中,小星利用无人机来测量广场 , 两点之间的距离.如图所示,小星站在广场的 处遥控无人机,无人机在 处距离地面的飞行高度是 ,此时从无人机测得广场 处的俯角为 ,他抬头仰视无人机时,仰角为 ,若小星的身高 , (点 , , , 在同一平面内).
(1)求仰角 的正弦值;
(2)求 , 两点之间的距离(结果精确到 .
, , , , ,
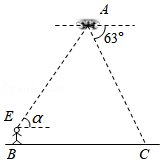
如图,一次函数 的图象与反比例函数 的图象交于点 ,与 轴交于点 ,过点 作 轴,垂足为 ,若 .
(1)求点 的坐标及 的值;
(2)若 ,求一次函数的表达式.
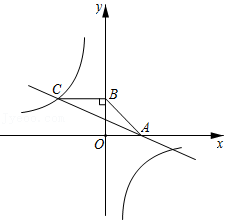
如图,在矩形 中,点 在 上, ,且 ,垂足为 .
(1)求证: ;
(2)若 , ,求四边形 的面积.