(本小题满分12分)
某小区要建一个面积为500平方米的矩形绿地,四周有小路,绿地长边外路宽5米,短边外路宽9米,怎样设计绿地的长与宽,使绿地和小路所占的总面积最小,并求出最小值.
|
(13分) 已知点A,B的坐标分别是(0,–1),(0,1),直线AM,BM相交于点M,且它们的斜率之积为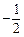 .(10求点M的轨迹C的方程;(2)过D(2,0)的直线l与轨迹C有两不同的交点时,求l的斜率的取值范围;(3)若过点D(2,0)的直线l与(1)中的轨迹C交于不同的两点E、F(E在D、F之间),试求
.(10求点M的轨迹C的方程;(2)过D(2,0)的直线l与轨迹C有两不同的交点时,求l的斜率的取值范围;(3)若过点D(2,0)的直线l与(1)中的轨迹C交于不同的两点E、F(E在D、F之间),试求 与
与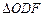 面积之比的取值范围(O为坐标原点);
面积之比的取值范围(O为坐标原点);
(13分) 已知曲线C: 的横坐标分别为1和
的横坐标分别为1和 ,且a1=5,数列{xn}满足xn+1 = tf (xn – 1) + 1(t > 0且
,且a1=5,数列{xn}满足xn+1 = tf (xn – 1) + 1(t > 0且 ).设区间
).设区间 ,当
,当 时,曲线C上存在点
时,曲线C上存在点 使得xn的值与直线AAn的斜率之半相等.
使得xn的值与直线AAn的斜率之半相等.
(1)证明: 是等比数列;
是等比数列;
(2)当

 对一切
对一切 恒成立时,求t的取值范围;
恒成立时,求t的取值范围;
(3)记数列{an}的前n项和为Sn,当 时,试比较Sn与n + 7的大小,并证明你的结论.
时,试比较Sn与n + 7的大小,并证明你的结论.
(13分) 已知函数 ,
,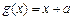 (a > 0)(1)求a的值,使点M(
(a > 0)(1)求a的值,使点M( ,
,  )到直线
)到直线 的最短距离为
的最短距离为 ;(2)若不等式
;(2)若不等式 在
在 [1,4]恒成立,求a的取值范围.
[1,4]恒成立,求a的取值范围.
(12分) 已知 ,
,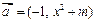 ,
, ,
,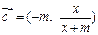 .
.
(1)当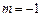 时,求使不等式
时,求使不等式 成立的x的取值范围;
成立的x的取值范围;
(2)当m﹥0时,求使不等式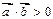 成立的x的取值范围.
成立的x的取值范围.
(12分) 已知向量 与
与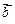 的夹角为30°,且|
的夹角为30°,且| |=
|= ,|
,|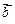 |=1,(1)求|
|=1,(1)求| -2
-2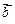 |的值;(2)设向量
|的值;(2)设向量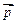 =
= +2
+2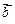 ,
, =
= -2
-2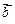 ,求向量
,求向量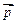 在
在 方向上的投影.
方向上的投影.