(本小题满分12分 )
)
已知二次函数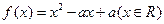 同时满足:
同时满足:
①不等式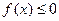 的解集有且只有一个元素;
的解集有且只有一个元素;
②在定义域内存在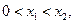 使得不等式
使得不等式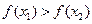 成立.
成立.
设数列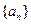 的前
的前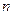 项和
项和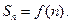
(1)求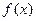 表达式;
表达式;
(2)求数列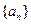 的通项公式;
的通项公式;
(3)设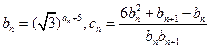 ,
,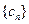 的前
的前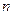 项和为
项和为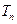 ,
,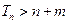 对
对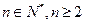
恒成立,求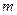 的取值范围.
的取值范围.
(本小题满分10分)如图,在四棱锥P-ABCD中,底面ABCD是正方形,
侧棱PD⊥底面ABCD,PD=DC,E是PC的中点.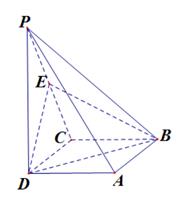
(1)求证:PA∥平面BDE;
(2)求证:平面BDE⊥平面PBC.
(本小题满分10分)设直线l的方程为(a+1)x+y+2-a=0(a∈R).
(1)若l在两坐标轴上截距相等,求l的方程;
(2)若l不经过第二象限,求实数a的取值范围.
(本小题满分13分)如图,在多面体ABCDEF中,正方形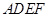 与梯形
与梯形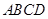 所在平面互相
所在平面互相
垂直, 已知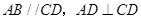 ,
,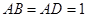 ,
, .
.
(Ⅰ)求证: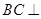 平面
平面 ;
;
(Ⅱ)求点C到平面BDF的距离.
(本小题满分13分)已知数列{an}的前n项和为Sn,又a1=1,a2=2,且满足Sn+1=kSn+1,
(1)求k的值及{an}的通项公式;
(2)若 ,求证:
,求证: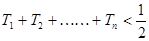 .
.
(本小题满分10分)设△ABC的内角A、B、C的对边长分别为a、b、c,设S为△ABC的面积,
满足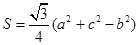 .
.
(Ⅰ)求B;
(Ⅱ)若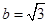 ,设
,设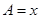 ,
,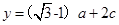 ,求函数
,求函数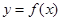 的解析式和最大值.
的解析式和最大值.