(本小题10分)在平面直角坐标系中,将直线l: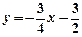 沿x轴翻折,得到一条新直线与x轴交于点A,与y轴交于点B,将抛物线
沿x轴翻折,得到一条新直线与x轴交于点A,与y轴交于点B,将抛物线 :
: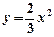 沿x轴平移,得到一条新抛物线
沿x轴平移,得到一条新抛物线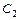 与y轴交于点D,与直线AB交于点E、点F.
与y轴交于点D,与直线AB交于点E、点F.
(Ⅰ)求直线AB的解析式;
(Ⅱ)若线段DF∥x轴,求抛物线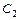 的解析式;
的解析式;
(Ⅲ)在(2)的条件下,若点F在y轴右侧,过F作FH⊥x轴于点G,与直线l交于点H,一条直线m(m不过△AFH的顶点)与AF交于点M,与FH交于点N,如果直线m既垂直于直线AB又平分△AFH的面积,求直线m的解析式.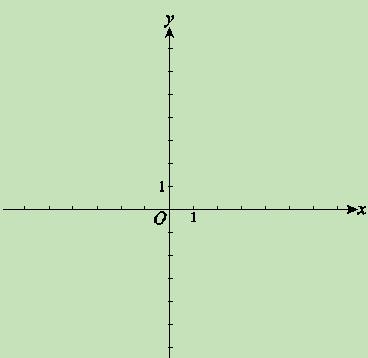
如图,正方形 中,
中, 与
与 分别是
分别是 、
、 上一点.在
上一点.在
①  、②
、②  ∥
∥ 、③
、③  中,
中,
选择其中一个条件,证明 .
.
已知一纸箱中放有大小均匀的 只白球和
只白球和 只黄球,从箱中随机地取出一只白球的概率是
只黄球,从箱中随机地取出一只白球的概率是 .
.写出
 与
与 的函数关系式;
的函数关系式;当
 时,再往箱中放进20只白球,求随机地取出一只黄球的概率
时,再往箱中放进20只白球,求随机地取出一只黄球的概率 .
.
如图,在直角坐标平面内, 为原点,点
为原点,点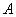 的坐标为
的坐标为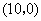 ,点
,点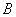 在第一象限内,
在第一象限内,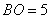 ,
, .
.求:点
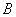 的坐标。
的坐标。求:
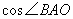 的值.
的值.
如图所示,将矩形 沿
沿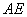 折叠,使点
折叠,使点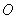 恰好落在
恰好落在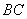 上
上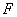 处,以
处,以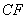 为边作正方形
为边作正方形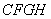 ,延长
,延长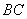 至
至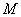 ,使
,使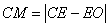 ,再以
,再以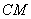 、
、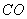 为边作矩形
为边作矩形 .
.试比较
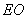 、
、 的大小,并说明理由.
的大小,并说明理由.令
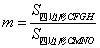 ,请问
,请问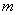 是否为定值?若是,请求出
是否为定值?若是,请求出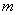 的值;若不是,请说明理由.
的值;若不是,请说明理由.在(2)的条件下,若
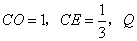 为
为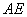 上一点且
上一点且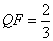 ,抛物线
,抛物线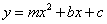 经过
经过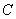 、
、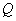 两点,请求出此抛物线的解析式.
两点,请求出此抛物线的解析式.在(3)的条件下,若抛物线
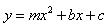 与线段
与线段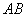 交于点
交于点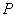 ,试问在直线
,试问在直线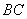 上是否存在点
上是否存在点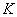 ,使得以
,使得以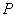 、
、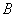 、
、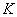 为顶点的三角形与
为顶点的三角形与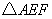 相似?若存在,请求直线
相似?若存在,请求直线 与
与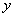 轴的交点
轴的交点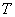 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.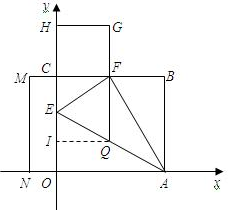
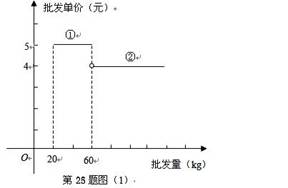
已知某种水果的批发单价与批发量的函数关系如图(1)所示.请说明图中①、②两段函数图象的实际意义;
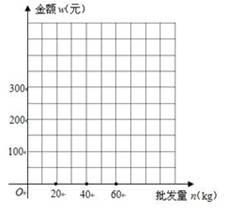
写出批发该种水果的资金金额w(元)与批发量n(kg)之间的函数关系式;在下图的坐标系中画出该函数图象;指出金额在什么范围内,以同样的资金可以批发到较多数量的该种水果.
经调查,某经销商销售该种水果的日最高销量与零售价之间的函数关系如图(2)所示,该经销商拟每日售出60kg以上该种水果,且当日零售价不变,请你帮助该经销商设计进货和销售的方案,使得当日获得的利润最大.