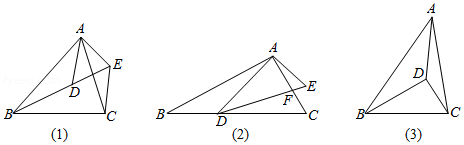
（11·十堰）如图，线段AD5，⊙A的半径为1，C为⊙A上一-优题课

5月20日九年级复学啦 $!$ 为了解学生的体温情况，班主任张老师根据全班学生某天上午的《体温监测记载表》，绘制了如下不完整的频数分布表和扇形统计图．

学生体温频数分布表

组别	温度 $(^{°} C)$	频数（人数）
甲	36.3	6
乙	36.4	$a$
丙	36.5	20
丁	36.6	4

请根据以上信息，答案下列问题：

（1）频数分布表中 $a =$ 　　，该班学生体温的众数是　　，中位数是　　；

（2）扇形统计图中 $m =$ 　　，丁组对应的扇形的圆心角是　　度；

（3）求该班学生的平均体温（结果保留小数点后一位）．

在平行四边形 $ABCD$ 中， $E$ 为 $AD$ 的中点，请仅用无刻度的直尺完成下列画图，不写画法，保留画图痕迹．

（1）如图1，在 $BC$ 上找出一点 $M$ ，使点 $M$ 是 $BC$ 的中点；

（2）如图2，在 $BD$ 上找出一点 $N$ ，使点 $N$ 是 $BD$ 的一个三等分点．

（1）先化简，再求值： $\frac{a^{2} - 4 a + 4}{a^{2} - 2 a} \div \frac{a^{2} - 4}{2 a}$ ，其中 $a = - 1$ ．

（2）解不等式组 $\{\begin{matrix} 3 x + 2 > x - 2 \\ \frac{x - 3}{3} ⩽ 7 - \frac{5}{3} x \end{matrix}$ ，并把它的解集在数轴上表示出来．

将抛物线 $C : y = {(x - 2)}^{2}$ 向下平移6个单位长度得到抛物线 $C_{1}$ ，再将抛物线 $C_{1}$ 向左平移2个单位长度得到抛物线 $C_{2}$ ．

（1）直接写出抛物线 $C_{1}$ ， $C_{2}$ 的解析式；

（2）如图（1），点 $A$ 在抛物线 $C_{1}$ （对称轴 $l$ 右侧）上，点 $B$ 在对称轴 $l$ 上， $ΔOAB$ 是以 $OB$ 为斜边的等腰直角三角形，求点 $A$ 的坐标；

（3）如图（2），直线 $y = kx (k \neq 0$ ， $k$ 为常数）与抛物线 $C_{2}$ 交于 $E$ ， $F$ 两点， $M$ 为线段 $EF$ 的中点；直线 $y = - \frac{4}{k} x$ 与抛物线 $C_{2}$ 交于 $G$ ， $H$ 两点， $N$ 为线段 $GH$ 的中点．求证：直线 $MN$ 经过一个定点．

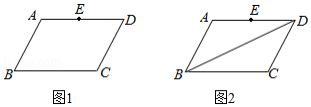
问题背景如图（1），已知 $ΔABC ∽ ΔADE$ ，求证： $ΔABD ∽ ΔACE$ ；

尝试应用如图（2），在 $ΔABC$ 和 $ΔADE$ 中， $∠ BAC = ∠ DAE = 90 °$ ， $∠ ABC = ∠ ADE = 30 °$ ， $AC$ 与 $DE$ 相交于点 $F$ ，点 $D$ 在 $BC$ 边上， $\frac{AD}{BD} = \sqrt{3}$ ，求 $\frac{DF}{CF}$ 的值；

拓展创新如图（3）， $D$ 是 $ΔABC$ 内一点， $∠ BAD = ∠ CBD = 30 °$ ， $∠ BDC = 90 °$ ， $AB = 4$ ， $AC = 2 \sqrt{3}$ ，直接写出 $AD$ 的长．