袋中有大小相同的4个红球,6个白球,每次从中摸取一球,每个球被取到的可
能性相同,现不放回地取3个球.
(1)求第三个取出红球的概率;
(2)求至少取到两个红球的概率;
(3)(理)用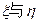 分别表示取得的红球数与白球数,计算
分别表示取得的红球数与白球数,计算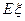 、
、 、
、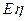 、
、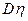 .
.
双曲线的中心在原点,焦点在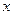 轴上,实轴长为4,它的两条渐近线与以
轴上,实轴长为4,它的两条渐近线与以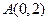 为圆心,1为半径的圆相切,直线
为圆心,1为半径的圆相切,直线 过点A与双曲线的右支交于B、C两点,
过点A与双曲线的右支交于B、C两点,
(1)求双曲线的方程;(2)若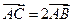 ,求直线
,求直线 的方程
的方程
如图:在四棱锥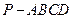 中,底面为菱形,
中,底面为菱形,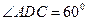 ,
,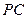 与底面
与底面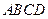 垂直,
垂直,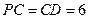 ,
, 为棱
为棱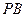 的中点,
的中点, 为
为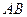 的中点,
的中点,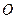 为
为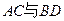 的交点,
的交点,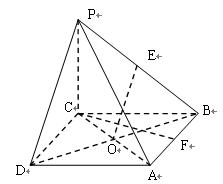
(1)求证: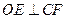 ;
;
(2)求锐二面角 的余弦值.
的余弦值.
抛物线 的焦点与椭圆
的焦点与椭圆 的一个焦点重合,且抛物线与椭圆的一个交点为
的一个焦点重合,且抛物线与椭圆的一个交点为 ,(1)求抛物线与椭圆的方程,(2)若过点
,(1)求抛物线与椭圆的方程,(2)若过点 的直线与抛物线交于点
的直线与抛物线交于点 ,求
,求 的最小值
的最小值
已知实数 ,命题
,命题 有两个不同的的实数根;
有两个不同的的实数根;
命题 。若
。若 为真,
为真, 为假,求
为假,求 的取值范围。
的取值范围。
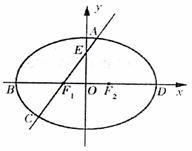
如图,在椭圆 中,F1,F2分别为椭圆的左、右焦点,B、D分别
中,F1,F2分别为椭圆的左、右焦点,B、D分别
为椭圆的左、右顶点,A为椭圆在第一象限内的一点,直线AF1交椭圆于另
一点C,交y轴于点E,且点F1、F2三等分线段BD.
(1)求 的值;
的值;
(2)若四边形EBCF2为平行四边形,求点C的坐标;
(3)当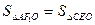 时,求直线AC的方程.
时,求直线AC的方程.