(本小题满分14分)
如图,四边形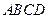 为矩形,且
为矩形,且 ,
,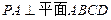 ,
, 为
为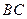 上的动点.
上的动点.
(1) 当 为
为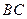 的中点时,求证:
的中点时,求证: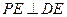 ;
;
(2) 设 ,在线段
,在线段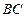 上存在这样的点E,使得二面角
上存在这样的点E,使得二面角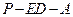 的平面角大小为
的平面角大小为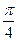 . 试确定点E的位置.
. 试确定点E的位置.
已知二次函数f(x)=ax2+bx+c和一次函数g(x)=-bx,其中a、b、c满足a>b>c,a+b+c=0,(a,b,c∈R)
(1)求证:两函数的图象交于不同的两点A、B;
(2)求线段AB在x轴上的射影A1B1的长的取值范围.
如图,直三棱柱ABC—A1B1C1,底面△ABC中,CA=CB=1,∠BCA=90°,AA1=2,M、N分别是A1B1、A1A的中点.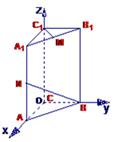
(1)求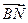 的长;
的长;
(2)求cos<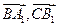 >的值;
>的值;
(3)求证: A1B⊥C1M.
有A、B、C三个盒子,其中一个内放有一个苹果,在三个盒子上各有一张纸条.
A盒子上的纸条写的是“苹果在此盒内”,
B盒子上的纸条写的是“苹果不在此盒内”,
C盒子上的纸条写的是“苹果不在A盒内”.
如果三张纸条中只有一张写的是真的,请问苹果究竟在哪个盒子里?
写出下列各命题的否定及其否命题,并判断它们的真假.
(1)若x、y都是奇数,则x+y是偶数;
(2)若xy=0,则x=0或y=0;
(3)若一个数是质数,则这个数是奇数.
已知关于x的实系数二次方程x2+ax+b=0有两个实数根α、β,
证明:|α|<2且|β|<2是2|a|<4+b且|b|<4的充要条件.