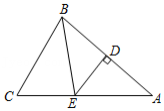
如图，在△ABC中，∠B60°，⊙O是△ABC外接圆，过点A-优题课

（1）计算： ${(- 1)}^{2} - {(π - 2021)}^{0} + | - \frac{1}{2} |$ ；

（2）如图，在 $ΔABC$ 中， $∠ A = 40 °$ ， $∠ ABC = 80 °$ ， $BE$ 平分 $∠ ABC$ 交 $AC$ 于点 $E$ ， $ED ⊥ AB$ 于点 $D$ ，求证： $AD = BD$ ．

甲、乙两汽车出租公司均有50辆汽车对外出租，下面是两公司经理的一段对话：

甲公司经理：如果我公司每辆汽车月租费3000元，那么50辆汽车可以全部租出．如果每辆汽车的月租费每增加50元，那么将少租出1辆汽车．另外，公司为每辆租出的汽车支付月维护费200元．

乙公司经理：我公司每辆汽车月租费3500元，无论是否租出汽车，公司均需一次性支付月维护费共计1850元．

说明：①汽车数量为整数；②月利润 $=$ 月租车费 $-$ 月维护费；③两公司月利润差 $=$ 月利润较高公司的利润 $-$ 月利润较低公司的利润．

在两公司租出的汽车数量相等的条件下，根据上述信息，解决下列问题：

（1）当每个公司租出的汽车为10辆时，甲公司的月利润是　 48000 　元；当每个公司租出的汽车为　　辆时，两公司的月利润相等；

（2）求两公司月利润差的最大值；

（3）甲公司热心公益事业，每租出1辆汽车捐出 $a$ 元 $(a > 0)$ 给慈善机构，如果捐款后甲公司剩余的月利润仍高于乙公司月利润，且当两公司租出的汽车均为17辆时，甲公司剩余的月利润与乙公司月利润之差最大，求 $a$ 的取值范围．

在一次数学探究活动中，李老师设计了一份活动单：

已知线段 $BC = 2$ ，使用作图工具作 $∠ BAC = 30 °$ ，尝试操作后思考：

（1）这样的点 $A$ 唯一吗？

（2）点 $A$ 的位置有什么特征？你有什么感悟？

“追梦”学习小组通过操作、观察、讨论后汇报：点 $A$ 的位置不唯一，它在以 $BC$ 为弦的圆弧上（点 $B$ 、 $C$ 除外）， $\dots$ ．小华同学画出了符合要求的一条圆弧（如图 $1)$ ．

（1）小华同学提出了下列问题，请你帮助解决．

①该弧所在圆的半径长为　　；

② $ΔABC$ 面积的最大值为　　；

（2）经过比对发现，小明同学所画的角的顶点不在小华所画的圆弧上，而在如图1所示的弓形内部，我们记为 $A'$ ，请你根据图1证明 $∠ BA' C > 30 °$ ．

（3）请你运用所学知识，结合以上活动经验，解决问题：如图2，已知矩形 $ABCD$ 的边长 $AB = 2$ ， $BC = 3$ ，点 $P$ 在直线 $CD$ 的左侧，且 $\tan ∠ DPC = \frac{4}{3}$ ．

①线段 $PB$ 长的最小值为　　；

②若 $S_{ΔPCD} = \frac{2}{3} S_{ΔPAD}$ ，则线段 $PD$ 长为　　．

如图，在平面直角坐标系中，二次函数 $y = x^{2} + bx + c$ 的图象与 $x$ 轴交于点 $A (- 1, 0)$ 、 $B (3, 0)$ ，与 $y$ 轴交于点 $C$ ．

（1） $b =$ 　　， $c =$ 　　；

（2）若点 $D$ 在该二次函数的图象上，且 $S_{ΔABD} = 2 S_{ΔABC}$ ，求点 $D$ 的坐标；

（3）若点 $P$ 是该二次函数图象上位于 $x$ 轴上方的一点，且 $S_{ΔAPC} = S_{ΔAPB}$ ，写出点 $P$ 的坐标．

如图，四边形 $ABCD$ 中， $AD / / BC$ ， $∠ BAD = 90 °$ ， $CB = CD$ ，连接 $BD$ ，以点 $B$ 为圆心， $BA$ 长为半径作 $⊙ B$ ，交 $BD$ 于点 $E$ ．

（1）试判断 $CD$ 与 $⊙ B$ 的位置关系，并说明理由；

（2）若 $AB = 2 \sqrt{3}$ ， $∠ BCD = 60 °$ ，求图中阴影部分的面积．