如图,在平面直角坐标系中,O是坐标原点,点A的坐标是(﹣4,0),点B的坐标是(0,b)(b>0).P是直线AB上的一个动点,作PC⊥x轴,垂足为C.记点P关于y轴的对称点为P´(点P´不在y轴上),连接PP´,P´A,P´C.设点P的横坐标为a.
(1)当b=3时,
①求直线AB的解析式;
②若点P′的坐标是(﹣1,m),求m的值;
(2)若点P在第一象限,记直线AB与P´C的交点为D.当P´D:DC=1:3时,求a的值;
(3)是否同时存在a,b,使△P´CA为等腰直角三角形?若存在,请求出所有满足要求的a,b的值;若不存在,请说明理由.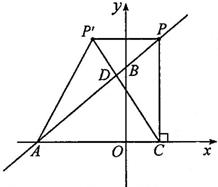
青年志愿者爱心小分队赴山村送温暖,准备为困难村民购买一些米面.已知购买1袋大米、4袋面粉,共需240元;购买2袋大米、1袋面粉,共需165元.
(1)求每袋大米和面粉各多少元?
(2)如果爱心小分队计划购买这些米面共40袋,总费用不超过2140元,那么至少购买多少袋面粉?
我省中小学积极开展综合实践活动,某校准备组织开展四项综合实践活动:“ .我是非遗小传人, .学做家常餐, .爱心义卖行动, .找个岗位去体验”.为了解学生最喜爱哪项综合实践活动,随机抽取部分学生进行问卷调查(每位学生只能选择一项),将调查结果绘制成下面两幅不完整的统计图,请结合图中提供的信息回答下列问题:
(1)本次一共调查了 名学生,在扇形统计图中, 的值是 ;
(2)补全条形统计图;
(3)若该校共有1200名学生,估计最喜爱 和 项目的学生一共有多少名?
(4)现有最喜爱 , , , 活动项目的学生各一人,学校要从这四人中随机选取两人交流活动体会,请用列表或画树状图的方法求出恰好选取最喜爱 和 项目的两位学生的概率.

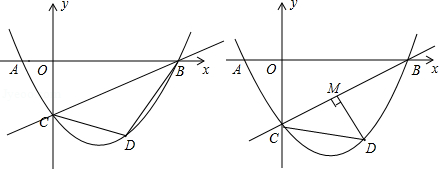
在平面直角坐标系中,直线 与 轴交于点 ,与 轴交于点 ,二次函数 的图象经过 , 两点,且与 轴的负半轴交于点 ,动点 在直线 下方的二次函数图象上.
(1)求二次函数的表达式;
(2)如图1,连接 , ,设 的面积为 ,求 的最大值;
(3)如图2,过点 作 于点 ,是否存在点 ,使得 中的某个角恰好等于 的2倍?若存在,直接写出点 的横坐标;若不存在,请说明理由.
如图1,以 的较短边 为一边作菱形 ,使点 落在边 上,连接 ,交 于点 .
(1)猜想 与 的数量关系,并说明理由;
(2)延长 、 交于点 ,其他条件不变:
①如图2,若 ,求 的值;
②如图3,若
,直接写出
的值(用含
的三角函数表示)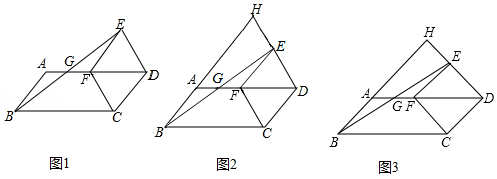
某商场销售一种商品,进价为每个20元,规定每个商品售价不低于进价,且不高于60元,经调查发现,每天的销售量 (个 与每个商品的售价 (元 满足一次函数关系,其部分数据如下所示:
|
每个商品的售价 (元 |
|
30 |
40 |
50 |
|
|
每天的销售量 (个 |
|
100 |
80 |
60 |
|
(1)求 与 之间的函数表达式;
(2)设商场每天获得的总利润为 (元 ,求 与 之间的函数表达式;
(3)不考虑其他因素,当商品的售价为多少元时,商场每天获得的总利润最大,最大利润是多少?