(本小题满分14分)数列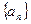 中,
中,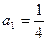 ;
; ,对任意的
,对任意的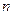 为正整数都有
为正整数都有 。
。
(1)求证: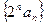 是等差数列;
是等差数列;
(2)求出
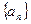 的通项公式
的通项公式 ;
;
(3)若 (
(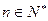 ),是否存在实数
),是否存在实数 使得
使得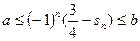 对任意的
对任意的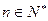 恒成立?若存在,找出
恒成立?若存在,找出 ;若不存在,请说明理由。
;若不存在,请说明理由。
(示范性高中做)
某公司计划在甲、乙两个仓储基地储存总量不超过300吨的一种紧缺原材料,总费用不超过9万元,此种原材料在甲、乙两个仓储基地的储存费用分别为 元/吨和200元/吨,假定甲、乙两个仓储基地储存的此种原材料每吨能给公司带来的收益分别为0.3万元和0.2万元
元/吨和200元/吨,假定甲、乙两个仓储基地储存的此种原材料每吨能给公司带来的收益分别为0.3万元和0.2万元 问该公司如何分配在甲、乙两个仓储基地的储存量,才能使公司的收益最大,最大收益是多少万元?
问该公司如何分配在甲、乙两个仓储基地的储存量,才能使公司的收益最大,最大收益是多少万元?
(本小题满分12分)
(普通高中做)
画出不等式组 所表示的平面区域(用阴影表示).若目标函数
所表示的平面区域(用阴影表示).若目标函数 ,求z的最大值.
,求z的最大值.
(本小题满分12分)
如图,在某平原地区一条河的彼岸有一建筑物,现在需要测量其高度AB.由于雨季河宽水急不能涉水,只能在此岸测量.现有的测量器材只有测角仪和皮尺.现在选定了一条水平基线HG,使得H、G、B三点在同一条直线上.请你设计一种测量方法测出建筑物的高度,并说明理由.(测角仪的高为h)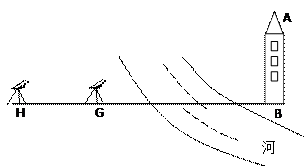
(方案二)如图是一个长方体被削去一部分后的多面体的直观图,它的正视图和侧视图已经画出.(单位:cm).
(Ⅰ)在正视图下面,按照画三视图的要求画出该多面体的俯视图;
(Ⅱ)(普通高中做)求三棱锥 的体积.
的体积.
(示范性高中做)求多面体 的体积.
的体积.
(本小题满分12分)
(方案一)已知: ,
,  与
与 的夹角为
的夹角为 ,
, (
( )当m为何值时,
)当m为何值时, 与
与 垂直?
垂直?