(本小题满分10分)
某地区为下岗女职工免费提供财会和家政培训,以提高下岗女职工的再就业能力,每名下岗人员可以参加一项培训、参加两项培训或不参加培训,已知参加过财会培训的有50%,参加过家政培训的有80%,假设每个人对培训项目的选择是相互独立的,且各人的选择相互之间没有影响
(1)任选1名下岗女职工,求该人参加过培训的概率
(2)任选3名下岗女职工,记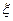 为3人中参加过培训的人数,求
为3人中参加过培训的人数,求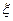 的分布列和期望
的分布列和期望
(本小题满分14分)
已知函数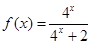 .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)若数列
 ,
,
求数列 的通项公式;
的通项公式;
(Ⅲ)若数列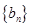 满足
满足 ,
, 是数列
是数列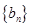 的前
的前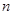 项和,是否存在正实数
项和,是否存在正实数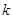 ,使不等式
,使不等式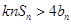 对于一切的
对于一切的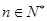 恒成立?若存在,请求出
恒成立?若存在,请求出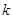 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
(本小题满分12分)
已知点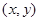 是区域
是区域 ,(
,(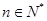 )内的点,目标函数
)内的点,目标函数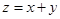 ,
, 的最大值记作
的最大值记作 .若数列
.若数列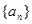 的前
的前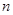 项和为
项和为 ,
, ,且点(
,且点( )在直线
)在直线 上.
上.
(Ⅰ)证明:数列 为等比数列;
为等比数列;
(Ⅱ)求数列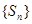 的前
的前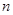 项和
项和 .
.
(本小题满分12分)
攀岩运动是一项刺激而危险的运动,如图(1)在某次攀岩活动中,两名运动员在如图所在位置,为确保运动员的安全,地面救援者应时刻注意两人离地面的距离,以备发生危险时进行及时救援. 为了方便测量和计算,画出示意图,如图(2)所示,点 分别为两名攀岩者所在位置,点
分别为两名攀岩者所在位置,点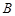 为山的拐角处,且斜坡AB的坡角为
为山的拐角处,且斜坡AB的坡角为 ,点
,点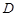 为山脚,某人在地面上的点
为山脚,某人在地面上的点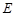 处测得
处测得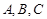 的仰角分别为
的仰角分别为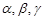 ,
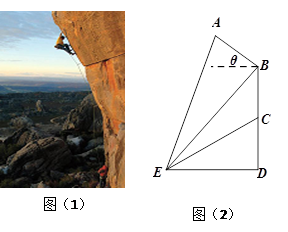
, 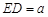 ,
,
求:(Ⅰ)点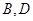 间的距离及点
间的距离及点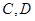 间的距离;
间的距离;
(Ⅱ)在点 处攀岩者距地面的距离
处攀岩者距地面的距离 .
.
(本小题满分10分)
福州市某大型家电商场为了使每月销售空调和冰箱获得的总利润达到最大,对某月即将出售的空调和冰箱进行了相关调查,得出下表:
| 资金 |
每台空调或冰箱所需资金(百元) |
月资金最多供应量 (百元) |
|
| 空调 |
冰箱 |
||
| 进货成本 |
30 |
20 |
300 |
| 工人工资 |
5 |
10 |
110 |
| 每台利润 |
6 |
8 |
问:如果根据调查得到的数据,该商场应该怎样确定空调和冰箱的月供应量,才能使商场获得的总利润最大?总利润的最大值为多少元?
(本小题满分12分)
已知关于 的不等式
的不等式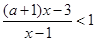 .
.
(Ⅰ)当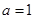 时,解该不等式;
时,解该不等式;
(Ⅱ)当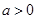 时,解该不等式.
时,解该不等式.