如图,正方形 的边长为1,正方形
的边长为1,正方形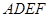 所在平面与平面
所在平面与平面 互相垂直,
互相垂直,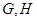 是
是 的中点.
的中点.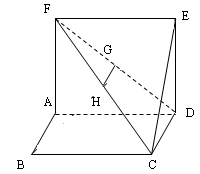
(1)求证: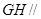 平面
平面 ;
;
(2)求证: ;
;
(3)求三棱锥 的体积.
的体积.
已知函数 的定义域为A,函数
的定义域为A,函数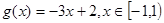 的值域为B,求
的值域为B,求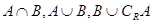
下面是对智商在40~69之间的人的出生季节所作的一项调查。结果如下(单位:人):
| 智商 季节 |
40~54 |
55~69 |
合计 |
| 夏和秋 |
20 |
30 |
50 |
| 春和冬 |
10 |
X |
50 |
| 合计 |
30 |
70 |
Y |
(Ⅰ) 请求出表中X和Y的值;
(Ⅱ) 问智商在40~69之间的人的智商与出生季节是否有关联?
设函数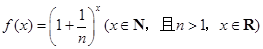
(Ⅰ)当 时,求
时,求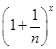 的展开式中二项式系数最大的项;
的展开式中二项式系数最大的项;
(Ⅱ)对任意的实数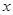 ,证明 :
,证明 :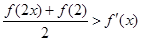 (
(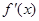 是
是 的导函数);
的导函数);
随机抽取某厂的某种产品100件,经质检,其中有一等品63件、二等品25件、三等品10件、次品2件.已知生产1件一、二、三等品获得的利润分别为6万元、2万元、1万元,而1件次品亏损2万元.设1件产品的利润(单位:万元)为 .
.
(1)求 的分布列;
的分布列;
(2)求1件产品的平均利润(即 的数学期望);
的数学期望);
(3)经技术革新后,仍有四个等级的产品,但次品率降为 ,一等品率提高为
,一等品率提高为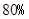 .如果此时要求1件产品的平均利润不小于5.13万元,则三等品率最多是多少?
.如果此时要求1件产品的平均利润不小于5.13万元,则三等品率最多是多少?
学校为绿化环境,移栽了甲、乙两种大树各2株.设甲、乙两种大树移栽的成活率分别为 和
和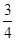 ,且各株大树是否成活互不影响.
,且各株大树是否成活互不影响.
(Ⅰ)求移栽的4株大树中恰有3株成活的概率;
(Ⅱ)设移栽的4株大树中成活的株数为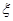 ,求
,求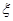 分布列与期望.
分布列与期望.