(本小题满分10分)选修4-4:坐标系与参数方程
已知曲线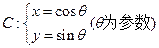 。
。
(Ⅰ)将曲线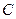 的参数方程化为普通方程;
的参数方程化为普通方程;
(Ⅱ)若把曲线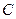 上各点的坐标经过伸缩变换
上各点的坐标经过伸缩变换 后得到曲线
后得到曲线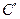 ,求曲线
,求曲线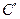 上任意一点到两坐标轴距离之积的最大值.
上任意一点到两坐标轴距离之积的最大值.
如图所示,正方形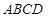 和矩形
和矩形 所在平面相互垂直,
所在平面相互垂直,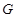 是
是 的中点.
的中点.
(I)求证: ;
;
(Ⅱ)若直线 与平面
与平面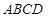 成45o角,求异面直线
成45o角,求异面直线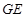 与
与 所成角的余弦值.
所成角的余弦值.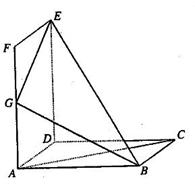
如图:已知平面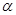 //平面
//平面 ,点A、B在平面
,点A、B在平面 内,点C、D在
内,点C、D在 内,直线AB与CD是异面直线,点E、F、G、H分别是线段AC、BC、BD、AD的中点,
内,直线AB与CD是异面直线,点E、F、G、H分别是线段AC、BC、BD、AD的中点,
求证:(Ⅰ)E、F、G、H四点共面;
(Ⅱ)平面EFGH//平面 .
.
如图,在正方体ABCD-A1B1C1D1中,E、F、G分别是CB、CD、CC1的中点,
求证:平面A B1D1∥平面EFG;
求二面角 的正切值。
的正切值。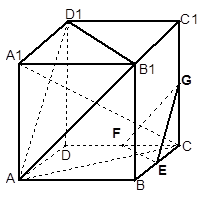
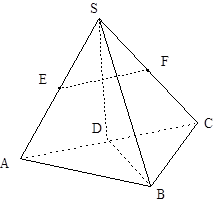
如图:在三棱锥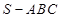 中,已知点
中,已知点 、
、 、
、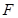 分别为棱
分别为棱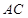 、
、 、
、 的中点.
的中点.
(Ⅰ)求证: ∥平面
∥平面 ;
;
(Ⅱ)若 ,
,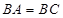 ,求证:平面
,求证:平面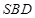 ⊥平面
⊥平面 .
.
已知直线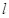 经过直线
经过直线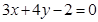 与直线
与直线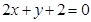 的交点
的交点 ,且垂直于直线
,且垂直于直线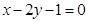 .
.
(Ⅰ)求直线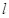 的方程;
的方程;
(Ⅱ)求直线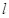 与两坐标轴围成的三角形的面积
与两坐标轴围成的三角形的面积