(本小题满分9分)某校为了了解九年级学生数学测试成绩情况,以九年级(1)
班学生的数学测试成绩为样本,按A,B,C,D四个等级进行统计,并将统计结果绘制如下两幅统计图,请你结合图中所给信息解答下列问题:
(说明:A级:108分~120分;B级:102分~107分;C级:72分~101分; D级: 72分以下)

(1)补全条形统计图并计算C级学生的人数占全班总人数的百分比;
(2)求出D级所在的扇形圆心角的度数;
(3)该班学生数学测试成绩的中位数落在哪个等级内;
(4)若102分以上(包括102分)为优秀,该校九年级学生共有1500人,请你估计这次考试中数学优秀的学生共有多少人?
如图所示的是夹文件用的铁(塑料)夹子在常态下的侧面示意图.AC,BC表示铁夹的两个面,O点是轴,OD⊥AC于点D,且AD=15mm,DC=24mm,OD=10mm.已知文件夹是轴对称图形,试利用图②,求图①中A,B两点间的距离.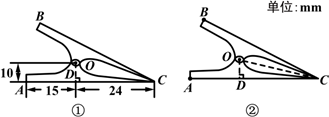
如图所示,花丛中有一路灯AB,在灯光下,小明在点D处的影子DE=3米,沿BD方向行5米走到点G,这时小明的影长HG=5米.如果小明的身高为1.7米,求路灯AB的高度.(精确到0.1米)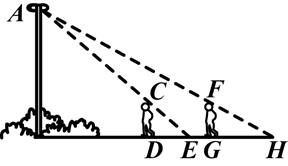
某市经济开发区建有B,C,D三个食品工厂,这三个工厂和开发区A处的自来水厂正好在一个矩形的四个顶点上,它们之间有公路相通,且AB=CD=900m,AD=BC=1700m,自来水公司已经修好一条自来水主管道AN,B,C两厂之间的公路与自来水主管道交于E处,EC=500m.若修建自来水主管道到各工厂的自来水管道由各厂负担,每米造价800元.
(1)要使修建自来水管道的造价最低,这三个工厂的自来水管道路线应怎样设计?并在图中画出.
(2)各厂所修建自来水管道的最低造价各是多少元?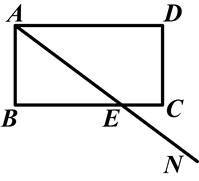
某一天,小明和小亮来到一河边,想用遮阳帽和皮尺测量这条河的大致宽度,两人在确保无安全隐患的情况下,先在河岸边选择了一点B(点B与河对岸岸边上的一棵树的底部点D所确定的直线垂直于河岸).
①小明在B点面向树的方向站好,调整帽檐,使视线通过帽檐正好落在树的底部点D处,如图所示,这时小亮测得小明眼睛距地面的距离AB=1.7米;
②小明站在原地转动180°后蹲下,并保持原来的观察姿态(除身体重心下移外,其他姿态均不变),这时视线通过帽檐落在了DB延长线上的点E处,此时小亮测得BE=9.6米,小明的眼睛距地面的距离CB=1.2米.
根据以上测量过程及测量数据,请你求出河宽BD是多少米.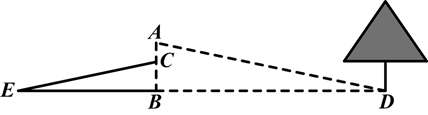
如图所示,一段街道的两边缘所在直线分别为AB,PQ,并且AB∥PQ,建筑物的一端DE所在的直线MN⊥AB于点M,交PQ于点N,小亮从胜利街的A处,沿着AB的方向前进,小明一直站在点P的位置等候小亮.
(1)请你在图中画出小亮恰好能看见小明时的视线,以及此时小亮所在的位置(用点C标出);
(2)已知MN=20m,MD=8m,PN=24m,求(1)中的点C到胜利街口的距离CM.