某一天,小明和小亮来到一河边,想用遮阳帽和皮尺测量这条河的大致宽度,两人在确保无安全隐患的情况下,先在河岸边选择了一点B(点B与河对岸岸边上的一棵树的底部点D所确定的直线垂直于河岸).
①小明在B点面向树的方向站好,调整帽檐,使视线通过帽檐正好落在树的底部点D处,如图所示,这时小亮测得小明眼睛距地面的距离AB=1.7米;
②小明站在原地转动180°后蹲下,并保持原来的观察姿态(除身体重心下移外,其他姿态均不变),这时视线通过帽檐落在了DB延长线上的点E处,此时小亮测得BE=9.6米,小明的眼睛距地面的距离CB=1.2米.
根据以上测量过程及测量数据,请你求出河宽BD是多少米.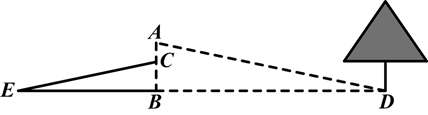
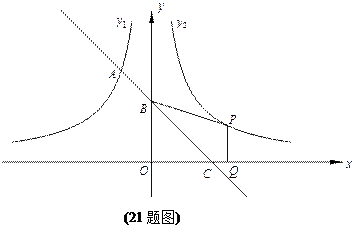
如图,一次函数的图象与反比例函数y1=" –" ( x<0)的图象相交于A点,与y轴、x轴分别相交于B、C两点,且C(2,0).当x<–1时,一次函数值大于反比例函数的值,当x>–1时,一次函数值小于反比例函数值.
(1)求一次函数的解析式;
(2)设函数y2= (x>0)的图象与y1=" –" (x<0)的图象关于y轴对称.在y2= (x>0)的图象上取一点P(P点的横坐标大于2),过P作PQ⊥x轴,垂足是Q,若四边形BCQP的面积等于2,求P点的坐标.
 |
某县为鼓励失地农民自主创业,在2010年对60位自主创业的失地农民自主创业的失地农民进行奖励,共计划奖励10万元.奖励标准是:失地农民自主创业连续经营一年以上的给予1000元奖励;自主创业且解决5人以上失业人员稳定就业一年以上的,再给予2000元奖励.问:该县失地农民中自主创业连续经营一年以上的和自主创业且解决5人以上失业人员稳定就业一年以上的农民分别有多少人?
某校开展了以“人生观、价值观”为主题的班队活动,活动结束后,初三(2)班数学兴趣小组提出了5个主要观点并在本班50名学生中进行了调查(要求每位同学只选自己最认可的一项观点),并制成了如下扇形统计图.
(1)该班学生选择“和谐”观点的有人,在扇形统计图中,“和谐”观点所在扇形区域的圆心角是度.
(2)如果该校有1500名初三学生,利用样本估计选择“感恩”观点的初三学生约有人.
(3)如果数学兴趣小组在这5个主要观点中任选两项观点在全校学生中进行调查,求恰好选到“和谐”和“感恩”观点的概率(用树状图或列表法分析解答)
 |
解不等式组,并把它的解集在数轴上表示出来.
(3)如图,平行四边形ABCD的对角线AC、BD交于点O,E、F在AC上,G、H在BD上,且AF=CE,BH=DG,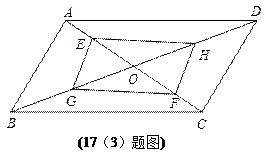 求证:AG∥HE
求证:AG∥HE