（本小题满分12分）
某网站就观众对2010年春晚小品类节目的喜爱程度进行网上调查，其中持各种态
度的人数如下表：
| 喜爱程度 |
喜欢 |
一般 |
不喜欢 |
| 人数 |
560 |
240 |
200 |
（1）现用分层抽样的方法从所有参与网上调查的观众中抽取了一个容量为n的样本，已知从不喜欢小品的观众中抽取的人数为5人，则n的值为多少？
（2）在（1）的条件下，若抽取到的5名不喜欢小品的观众中有2名为女性，现将抽取到的5名不喜欢小品的观众看成一个总体 ，从中任选两名观众，求至少有一名为女性观众的概率.
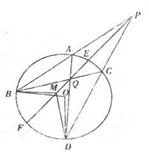
如图,过圆O外一点P作该圆的两条割线PAB和PCD,分别交圆 O于点A,B,C,D弦AD和BC交于Q点，割线PEF经过Q点交圆 O于点E、F，点M在EF上，且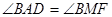
:
(I)求证:PA·PB=PM·PQ；(II)求证：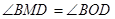
.
(本小题满分12分）
已知函数f(x)=ex+ax-1(e为自然对数的底数).
（Ⅰ）当a=1时,求过点（1,f(1))处的切线与坐标轴围成的三角形的面积；
(II)若f(x)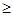
x2在(0,1 )上恒成立,求实数a的取值范围.
椭圆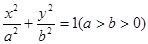
的左、右焦点分别为F1(-1，0)，F2(1,0)，过F1作与x轴不重合的直线l交椭圆于A,B两点.
（Ⅰ）若ΔABF2为正三角形，求椭圆的离心率；
（Ⅱ）若椭圆的离心率满足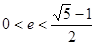
,0为坐标原点，求证
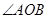为钝角.
为了调查某大学学生在周日上网的时间，随机对1OO名男生和100名女生进行了不记 名的问卷调查.得到了如下的统计结果：
表1:男生上网时间与频数分布表
表2:女生上网时间与频数分布表
(I)若该大学共有女生750人,试估计其中上网时间不少于60分钟的人数；
(II)完成下面的2x2列联表，并回答能否有90%的把握认为“学生周日上网时间与性 别有关”？
表3：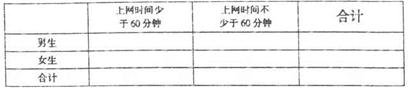
如图，在四棱锥P-ABCD中，PA丄平面ABCD，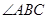
=
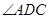=90°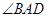
=1200,AD=AB=1,AC交BD于 O 点.
(I)求证:平面PBD丄平面PAC；
(Ⅱ)求三棱锥D-ABP和三棱锥B-PCD的体积之比.