(本小题满分9分)
如图,在直角坐标系中,点A的坐标为(-2,0),连结OA,将线段OA绕原点O顺时针旋转120°,得到线段OB.
(1)求经过A、O、B三点的抛物线的解析式;
(2)在(2)中抛物线的对称轴上是否存在点C,使△BOC的周长最小?若存在,求出点C的坐标;若不存在,请说明理由.
(3)如果点P是(2)中的抛物线上的动点,且在x轴的下方,那么△PAB是否有最大面积?若有,求出此时P点的坐标及△PAB的最大面积;若没有,请说明理由.
请认真阅读题意,并根据你的发现填空:
(1)将任何一组已知的勾股数中的每一个数都扩大为原来的正整数倍后,就得到一组新的勾股数,例如:3、4、5,我们把每一个数扩大为原来的2倍、3倍,则分别得到6、8、10和9、12、15,
若把每一个数都扩大为原来的12倍,就得到______________,
若把每一数都扩大为原来的n(n为正整数)倍,则得到_________________;
(2)对于任意一个大于1的奇数,存在着下列勾股数
若勾股数为3、4、5.则有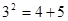
若勾股数为5、12、13, 则有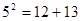
若勾股数为7、24、25, 则有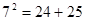
若勾股数为m(m为奇数)、n、______
则有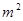 =2n+1,用m表示n=_______
=2n+1,用m表示n=_______
当m=17时,n=_______,此时勾股数为_______________.
△ABC中,AC=8,BC=6,在△ABE中,DE为AB边上的高,DE=12,S△ABE=60,求∠C的度数.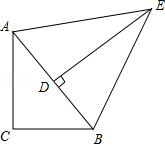
已知:如图,D、E、F是△ABC各边的中点,FG∥CD交ED的延长线于点G,AC=6,求GD的长度
已知:如图,双曲线 的图象经过A(1,2)、B(2,b)两点.
的图象经过A(1,2)、B(2,b)两点.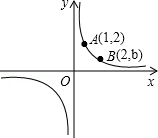
(1)求双曲线的解析式;
(2)当1<x<2时,反比例函数函数值的取值范围.
农机厂职工到距该厂15千米的向阳村检修农机,一部分人骑自行车先走,过了40分钟,其余人乘汽车去,结果他们同时到达。已知汽车的速度是自行车的3倍,求两种车的速度.