(本小题满分12分)
围建一个面积为360m2的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需维修),其它三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2m的进出口,已知旧墙的维修费用为45元/m,新墙的造价为180元/m,设利用的旧墙的长度为x(单位:元)。(Ⅰ)将总费用y表示为x的函数
(Ⅱ)试确定x,使修建此矩形场地围墙的总费用最小,并求出最小总费用
在 中,
中, 为锐角,角
为锐角,角 所对的边分别为
所对的边分别为 ,且
,且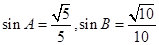
(I)求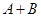 的值;
的值;
(II)若 ,求
,求 的值.
的值.
为了比较注射A, B两种药物后产生的皮肤疱疹的面积,选200只家兔做试验,将这200只家兔随机地分成两组,每组100只,其中一组注射药物A,另一组注射药物B.
(Ⅰ)甲、乙是200只家兔中的2只,求甲、乙分在不同组的概率;
(Ⅱ)下表1和表2分别是注射药物A和B后的试验结果.(疱疹面积单位:mm2)
表1:注射药物A后皮肤疱疹面积的频数分布表

完成答题卡中2×2列联表,并回答能否在犯错率不超过0.01%的前提下认为“注射药物A后的疱疹面积与注射药物B后的疱疹面积有差异”.
已知函数
(Ⅰ)求不等式 的解集;
的解集;
(Ⅱ)若关于x的不等式 恒成立,求实数
恒成立,求实数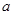 的取值范围.
的取值范围.
已知函数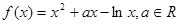
(1)若函数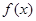 在[1,2]上是减函数,求实数
在[1,2]上是减函数,求实数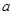 的取值范围;
的取值范围;
(2)令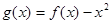 ,是否存在实数
,是否存在实数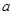 ,当
,当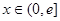 时,函数
时,函数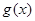 的最小值是3,若存在,求出
的最小值是3,若存在,求出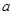 的取值;若不存在,说明理由.
的取值;若不存在,说明理由.
已知函数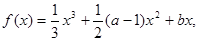 (
( 为常数)在
为常数)在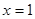 和
和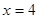 处取得极值,
处取得极值,
(1)求函数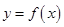 的解析式;
的解析式;
(2)当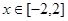 时,
时,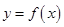 的图像恒在直线
的图像恒在直线 的下方,求实数
的下方,求实数 的取值范围.
的取值范围.