(本小题满分16分)
已知函数 (
( 是自然对数的底数).
是自然对数的底数).
(1)若曲线 在
在 处的切线也是抛物线
处的切线也是抛物线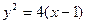 的切线,求
的切线,求 的值;
的值;
(2)若对于任意 恒成立,试确定实数
恒成立,试确定实数 的取值范围;
的取值范围;
(3)当 时,是否存在
时,是否存在 ,使曲线
,使曲线 在点
在点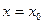 处的切线斜率与
处的切线斜率与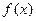 在
在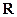 上的最小值相等?若存在,求符合条件的
上的最小值相等?若存在,求符合条件的 的个数;若不存在,请说明理由.
的个数;若不存在,请说明理由.
某市城调队就本地居民的月收入调查了10000人, 并根据所得数据画出了样本的频率分布直方图(每个分组包括左端点, 不包括右端点, 如第一组表示收入在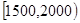 , 单位: 元).
, 单位: 元).
(Ⅰ)求随机抽取一位居民,估计该居民月收入在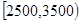 的概率,并估计这10000人的人均月收入;
的概率,并估计这10000人的人均月收入;
(Ⅱ)若将频率视为概率,从本地随机抽取3位居民(看作有放回的抽样),求月收入在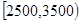 上居民人数
上居民人数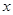 的数学期望.
的数学期望.
如图1,在Rt 中,
中,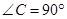 ,
,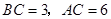 ,D、E分别是
,D、E分别是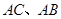 上的点,且
上的点,且 ,将
,将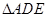 沿
沿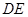 折起到
折起到 的位置,使
的位置,使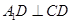 ,如图2.
,如图2.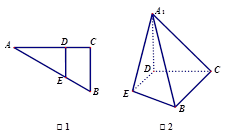
(Ⅰ)求证:平面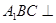 平面
平面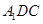 ;
;
(Ⅱ)若 ,求
,求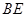 与平面
与平面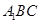 所成角的余弦值;
所成角的余弦值;
(Ⅲ)当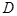 点在何处时,
点在何处时,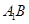 的长度最小,并求出最小值.
的长度最小,并求出最小值.
在数列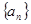 中,
中,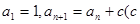 为常数,
为常数, ,且
,且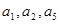 成公比不等于1的等比数列.
成公比不等于1的等比数列.
(Ⅰ)求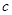 的值;
的值;
(Ⅱ)设 ,求数列
,求数列 的前
的前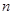 项和
项和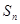 .
.
已知函数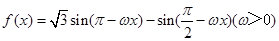 的图像上两相邻最高点的坐标分别为
的图像上两相邻最高点的坐标分别为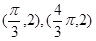 .
.
(Ⅰ)求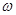 的值;
的值;
(Ⅱ)在△ABC中,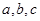 分别是角A,B,C的对边,且
分别是角A,B,C的对边,且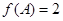 求
求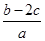 的取值范围.
的取值范围.
已知数列 具有性质:①
具有性质:① 为整数;②对于任意的正整数
为整数;②对于任意的正整数 ,当
,当 为偶数时,
为偶数时, ;当
;当 为奇数时,
为奇数时, .
.
(1)若 为偶数,且
为偶数,且 成等差数列,求
成等差数列,求 的值;
的值;
(2)设 (
( 且
且 N),数列
N),数列 的前
的前 项和为
项和为 ,求证:
,求证: ;
;
(3)若 为正整数,求证:当
为正整数,求证:当 (
( N)时,都有
N)时,都有 .
.