【改编】（本小题满分10分）
数形结合作为一种数学思想方法，数形结合的应用大致又可分为两种情形：或者借助于数的精确性来阐明形的某些属性，即“以数解形”；或者借助形的
几何直观性来阐明数之间的某种关系，即“以形助数”。 如浙教版九上课本第109页作业题第2题：如图1，已知在△ABC中，∠ACB=900，CD⊥AB，D为垂足。易证得两个结论：(1)AC·BC = AB·CD (2)AC2= AD·AB
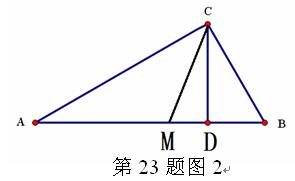
（1）请你用数形结合的“以数解形”思想来解：如图2，已知在△ABC中（AC>BC），∠ACB=900，CD⊥AB，D为垂足， CM平分∠ACB,且BC、AC是方程x2-14x+48=0的两个根，求AD、MD的长。
（2）请你用数形结合的“以形助数”思想来解：设a、b、c、d都是正数，满足a：b=c：d,且a最大。求证：a+d>b+c（提示：不访设AB=a,CD=d,AC=b,BC=c，构造图1）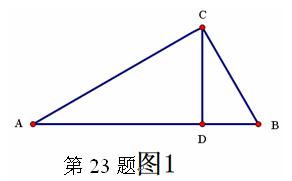
某商场出售的A型冰箱每台售价2190元，每日耗电量为1度，而B型节能冰箱每台售价虽比A型冰箱高出10%，但是每日耗电量却为0.55度，现将A型冰箱打折出售，问商场至少打几折，消费者购买才合算？（按使用期为10年，每年365天，每度电费按0.40元计算）
某企业生产一种产品，每件成本是400元，销售价为510元，本季度销售300件，为进一步扩大市场，企业决定在降低销售价的同时降低生产成本，经过市场调研，预测下季度这种产品每件销售价降低4%，销售量将提高10%，要使销售利润保持不变，该产品每件成本应降低多少元？
阅读下列材料再解方程：
│x+2│=3，我们可以将x+2视为一个整体，由于绝对值为3的数有两个，所以x+2=3或x+2=－3，解得x=1或－5．
请按照上面解法解方程x－│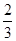
x+1│=1．
育红学校七年级学生步行到郊外旅行，七（1）班的学生组成前队，步行速度为4千米/时，七（2）班的学生组成后队，速度为6千米/时，前队出发1小时后，乙队才出发，同时后队派一名联络员骑自行车在两队之间不间断地来回联络，他骑车的速度为12千米/时，根据上面的事实提出问题并尝试去解答．
为了庆祝中国足球队首次进入世界杯赛，曙光体育器材厂赠送一批足球给希望中学足球队．若足球队每人领一个少6个球，每两人领一个则余6个球，问这批足球共多少个？小明领到足球后十分高兴，就仔细地研究起足球上的黑白球（如图），结果发现，黑块呈五边形，白色呈六边形，黑白相间在球体上，黑块共12块，问白块有多少块？