(本小题满分12分)
(理)已知甲,乙两名射击运动员各自独立地射击1次,命中10环的概率分别为 ,x(x>
,x(x> );且乙运动员在2次独立射击中恰有1次命中10环的概率为
);且乙运动员在2次独立射击中恰有1次命中10环的概率为
(I)求x的值
(II)若甲,乙两名运动员各自独立地射击1次,设两人命中10环的次数之和为随机变量ξ,求ξ的分布列及数学期望
已知圆C :(x-1)2+(y-2)2=2,点P坐标为(2,-1),过点P作圆C的切线,切点为A、B.
(1)求直线PA,PB的方程;
(2)求切线长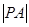 的值;
的值;
(3)求直线AB的方程.
如图,已知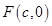 是椭圆
是椭圆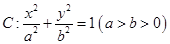 的右焦点;圆
的右焦点;圆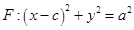 与
与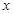 轴交于
轴交于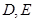 两点,其中
两点,其中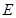 是椭圆
是椭圆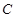 的左焦点.
的左焦点.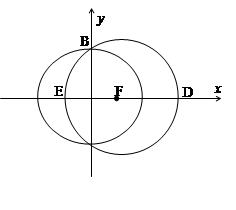
(1)求椭圆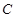 的离心率;
的离心率;
(2)设圆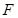 与
与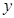 轴的正半轴的交点为
轴的正半轴的交点为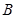 ,直线
,直线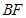 与圆
与圆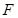 交于另一点
交于另一点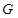 ,若
,若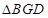 的面积为
的面积为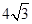 ,求椭圆
,求椭圆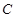 的标准方程.
的标准方程.
在平面直角坐标系xOy中,抛物线C的顶点在原点,经过点A(2,2),其焦点F在x轴上.
(1)求抛物线C的标准方程;
(2)设直线l是抛物线的准线,直线AF与抛物线交于另一点B,求证:以AB为直径的圆与准线l相切.
已知直线l与两坐标轴围成的三角形的面积为3,分别求满足下列条件的直线l的方程:
(1)过定点A(-3,4);
(2)斜率为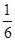 .
.
设椭圆C: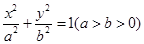 的左、右焦点分别为F1,F2,上顶点为A,过点A与AF2垂直的直线交x轴负半轴于点Q,且
的左、右焦点分别为F1,F2,上顶点为A,过点A与AF2垂直的直线交x轴负半轴于点Q,且 .
.
(1)求椭圆C的离心率;
(2)若过A、Q、F2三点的圆恰好与直线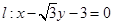 相切,求椭圆C的方程;
相切,求椭圆C的方程;
(3)在(2)的条件下,过右焦点F2作斜率为k的直线l与椭圆C交于M、N两点,在x轴上是否存在点P(m,0)使得以PM,PN为邻边的平行四边形是菱形,如果存在,求出m的取值范围,如果不存在,说明理由.