(本小题满分14分)
已知函数
(Ⅰ)写出函数的单调递减区间;
(Ⅱ)设 ,
,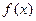 的最小值是
的最小值是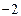 ,最大值是
,最大值是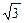 ,求实数
,求实数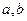 的值.
的值.
在如图所示的几何体中,四边形 是正方形,
是正方形, ⊥平面
⊥平面 ,
, ∥
∥ ,
,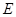 、
、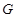 、
、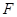 分别为
分别为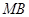 、
、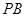 、
、 的中点,且
的中点,且 .
.
(1)求证:平面 ⊥平面
⊥平面 ;
;
(2)求三棱锥 与四棱锥
与四棱锥 的体积之比.
的体积之比.
如图是某直三棱柱(侧棱与底面垂直)被削去上底后的直观图与三视图中的侧(左)视图、俯视图,在直观图中, 是
是 的中点,侧(左)视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.
的中点,侧(左)视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.
(1)求出该几何体的体积;
(2)若 是
是 的中点,求证:
的中点,求证: ∥平面
∥平面 ;
;
(3)求证:平面 ⊥平面
⊥平面 .
.
如图,在直角梯形 中,
中,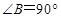 ,
,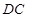 ∥
∥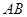 ,
, ,
,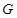 为线段
为线段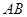 的中点,将
的中点,将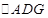 沿
沿 折起,使平面
折起,使平面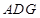 ⊥平面
⊥平面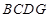 ,得到几何体
,得到几何体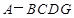 .
.
(1)若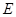 ,
, 分别为线段
分别为线段 ,
, 的中点,求证:
的中点,求证: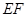 ∥平面
∥平面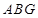 ;
;
(2)求证: ⊥平面
⊥平面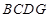 ;
;
(3)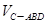 的值.
的值.
设函数f(x)=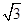 cos2ωx+sinωxcosωx+a(其中ω>0,a∈R),且f(x)的图象在y轴右侧的第一个最高点的横坐标为
cos2ωx+sinωxcosωx+a(其中ω>0,a∈R),且f(x)的图象在y轴右侧的第一个最高点的横坐标为 .
.
(1)求ω的值;
(2)如果f(x)在区间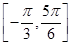 上的最小值为
上的最小值为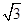 ,求a的值.
,求a的值.
已知向量m=(sinA,cosA),n=(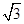 ,-1),m·n=1,且A为锐角.
,-1),m·n=1,且A为锐角.
(1)求角A的大小;
(2)求函数f(x)=cos2x+4cosAsinx(x∈R)的值域.