.本小题满分15分)
如图,已知椭圆E:
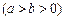 ,焦点为
,焦点为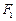 、
、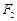 ,双曲线G:
,双曲线G: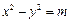
 的顶点是该椭
的顶点是该椭 圆的焦点,设
圆的焦点,设 是双曲线G上异于顶点的任一点,直线
是双曲线G上异于顶点的任一点,直线 、
、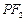 与椭圆的交点分别为A、B和C、D,已知三角形
与椭圆的交点分别为A、B和C、D,已知三角形 的周长等于
的周长等于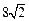 ,椭圆四个顶点组成的菱形的面积为
,椭圆四个顶点组成的菱形的面积为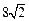 .
.
(1)求椭圆E与双曲线G的方程;
(2)设直线 、
、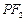 的斜率分别为
的斜率分别为 和
和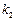 ,探求
,探求 和
和
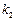 的关系;
的关系;
(3)是否存在常数 ,使得
,使得 恒成立?
恒成立?
若存在,试求出 的值;若不存在, 请说明理由.
的值;若不存在, 请说明理由.
已知函数f(x)=ex,x∈R.
(1)若直线y=kx+1与f(x)的反函数的图像相切,求实数k的值;
(2)设x>0,讨论曲线y=f(x)与曲线y=mx2(m>0)公共点的个数.
设函数f(x)=x2+aln(x+1)有两个极值点x1,x2,且x1<x2.
(1)求实数a的取值范围;
(2)当a=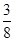 时,判断方程f(x)=-
时,判断方程f(x)=-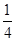 的实数根的个数,并说明理由.
的实数根的个数,并说明理由.
一家商场为了确定营销策略,进行了投入促销费用x和商场实际销售额y的试验,得到如下四组数据.
| 投入促销费用x(万元) |
2 |
3 |
5 |
6 |
| 商场实际营销额y(万元) |
100 |
200 |
300 |
400 |
(1)在下面的直角坐标系中,画出上述数据的散点图,并据此判断两个变量是否具有较好的线性相关性;
(2)求出x,y之间的回归直线方程 =
= x+
x+ ;
;
(3)若该商场计划营销额不低于600万元,则至少要投入多少万元的促销费用?
随机抽取某中学甲乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图所示.
(1)根据茎叶图判断哪个班的平均身高较高;
(2)计算甲班样本的方差.
公安部交管局修改后的酒后违法驾驶机动车的行为分成两个档次:“酒后驾车”和“醉酒驾车”,其判断标准是驾驶人员每100毫升血液中的酒精含量X毫克,当20≤X<80时,认定为酒后驾车;当X≥80时,认定为醉酒驾车,重庆市公安局交通管理部门在对G42高速路我市路段的一次随机拦查行动中,依法检测了200辆机动车驾驶员的每100毫升血液中的酒精含量,酒精含量X(单位:毫克)的统计结果如下表:
| X |
[0,20) |
[20,40) |
[40,60) |
[60,80) |
[80,100) |
[100,+∞) |
| 人数 |
t |
1 |
1 |
1 |
1 |
1 |
依据上述材料回答下列问题:
(1)求t的值;
(2)从酒后违法驾车的司机中随机抽取2人,求这2人中含有醉酒驾车司机的概率.