公安部交管局修改后的酒后违法驾驶机动车的行为分成两个档次：“酒后驾车”和“醉酒驾车”，其判断标准是驾驶人员每100毫升血液中的酒精含量X毫克，当20≤X<80时，认定为酒后驾车；当X≥80时，认定为醉酒驾车，重庆市公安局交通管理部门在对G42高速路我市路段的一次随机拦查行动中，依法检测了200辆机动车驾驶员的每100毫升血液中的酒精含量，酒精含量X(单位：毫克)的统计结果如下表：
| X |
[0，20) |
[20，40) |
[40，60) |
[60，80) |
[80，100) |
[100，＋∞) |
| 人数 |
t |
1 |
1 |
1 |
1 |
1 |
依据上述材料回答下列问题：
(1)求t的值；
(2)从酒后违法驾车的司机中随机抽取2人，求这2人中含有醉酒驾车司机的概率．
（本小题满分14分）
已知定义在R上的函数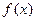
和数列
，当
时，
，其中
均为非零常数．
（Ⅰ）若数列
是等差数列，求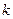
的值；
（Ⅱ）令
，求数列
的通项公式；
（Ⅲ）若数列为等比数列，求函数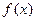的解析式．
（本小题满分13分）
已知椭圆
经过点
，离心率为
，动点
（Ⅰ）求椭圆的标准方程；
（Ⅱ）求以OM为直径且被直线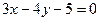
截得的弦长为2的圆的方程；
（Ⅲ）设F是椭圆的右焦点，过点F作OM的垂线与以OM为直径的圆交于点N，证明线段ON的长为定值，并求出这个定值．
（本小题满分13分）
已知函数
（Ⅰ）当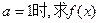
在区间
上的最大值和最小值；
（Ⅱ）若在区间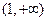
上，函数
的图象恒在直线
下方，求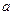
的取值范围．
（本小题满分14分）
在棱长为2的正方体ABCD—A1B1C1D1中，E，F分别为A1D1和CC1的中点．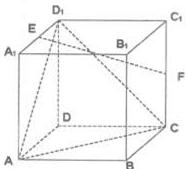
（Ⅰ）求证：EF//平面ACD1；
（Ⅱ）求异面直线EF与AB所成的角的余弦值；
（Ⅲ）在棱BB1上是否存在一点P，使得二面角P—AC—B的大小为30°？若存在，求出BP的长；若不存在，请说明理由．
（本小题满分13分）
为增强市民的节能环保意识，某市面向全市征召义务宣传志愿者，从符合条件的500名志愿者中随机抽样100名志原者的年龄情况如下表所示。
（Ⅰ）频率分布表中的①、②位置应填什么数据？并在答题卡中补全频率分布直方图（如图），再根据频率分布直方图估计这500名志愿者中年龄在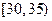
岁的人数；
（Ⅱ）在抽出的100名志原者中按年龄再采用分层抽样法抽取20人参加中心广场的宣传活动，从这20人中选取2名志愿者担任主要负责人，记这2名志愿者中“年龄低于30岁”的人数为X，求X的分布列及数学期望。