.已知函数f(x)= 在[0,1]上的最小值为
在[0,1]上的最小值为 ,
,
(1)求f(x)的解析式;(2)证明:f(1)+f(2)+…+f(n)>n- +
+ (n∈N
(n∈N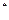 )
)
对于定义域为D的函数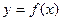 ,若同时满足下列条件:
,若同时满足下列条件:
①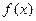 在D内单调递增或单调递减;
在D内单调递增或单调递减;
②存在区间[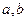 ]
]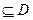 ,使
,使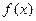 在[
在[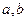 ]上的值域为[
]上的值域为[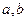 ];那么把
];那么把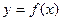 (
(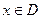 )叫闭函数。
)叫闭函数。
(1)求闭函数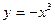 符合条件②的区间[
符合条件②的区间[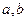 ];
];
(2)判断函数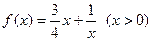 是否为闭函数?并说明理由;
是否为闭函数?并说明理由;
(3)若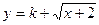 是闭函数,求实数
是闭函数,求实数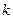 的取值范围。
的取值范围。
F1、F2为双曲线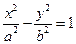 的左右焦点,O为坐标原点,P在双曲线的左支上,点M在右准线上,且满足:
的左右焦点,O为坐标原点,P在双曲线的左支上,点M在右准线上,且满足: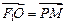 ,
,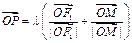 (λ>0)
(λ>0)
(1)求此双曲线的离心率;
(2)若过点N(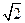 ,
,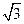 )的双曲线C的虚轴端点分别为B1、B2(B1在y轴正半轴上),点A、B在双曲线上,且
)的双曲线C的虚轴端点分别为B1、B2(B1在y轴正半轴上),点A、B在双曲线上,且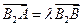 ,
,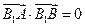 ,求双曲线C和直线AB的方程。
,求双曲线C和直线AB的方程。
已知函数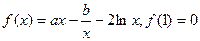 ,
,
(1)若函数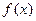 在其定义域内为单调函数,求
在其定义域内为单调函数,求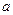 的取值范围;
的取值范围;
(2)若函数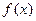 的图象在
的图象在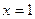 处的切线的斜率为0,且
处的切线的斜率为0,且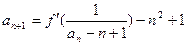 , 已知
, 已知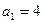 ,求证:
,求证: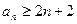
对于函数  ,若存在
,若存在 ,使
,使  成立,则称
成立,则称 为
为 的“滞点”.已知函数f ( x ) =
的“滞点”.已知函数f ( x ) =  .
.
(I)试问 有无“滞点”?若有,求之,否则说明理由;
有无“滞点”?若有,求之,否则说明理由;
(II)已知数列 的各项均为负数,且满足
的各项均为负数,且满足 ,求数列
,求数列 的通项公式;
的通项公式;
(III)已知 ,求
,求 的前项和
的前项和 .
.