在某次测验中,有6位同学的平均成绩为75分.用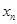 表示编号为
表示编号为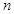 (
( )的同学所得成绩,且前5位同学的成绩如下:70,76,72,70,72.
)的同学所得成绩,且前5位同学的成绩如下:70,76,72,70,72.
(1)求第6位同学的成绩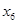 ,及这6位同学成绩的标准差
,及这6位同学成绩的标准差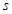 ;
;
(2)从前5位同学中,随机地选2位同学,求恰有1位同学成绩在区间(68,75)中的概率.
如图所示,在三棱柱 中,
中,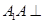 底面
底面 ,点
,点 在平面
在平面 中的投影为线段
中的投影为线段 上的点
上的点 .
.
(1)求证: ⊥
⊥
(2)点 为
为 上一点,若
上一点,若 ,
,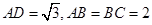 ,求三棱锥
,求三棱锥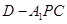 的体积.
的体积.
新华中学高三年级(1)班有甲,乙两个数学学习小组,每组抽选 名同学参加学校数学测试,成绩(满分
名同学参加学校数学测试,成绩(满分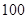 分)的茎叶图如图所示,其中甲组的平均成绩是
分)的茎叶图如图所示,其中甲组的平均成绩是 ,乙组成绩的中位数是
,乙组成绩的中位数是 .
.
(1)求茎叶图中 ,
,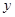 的值,且分别求出甲,乙两组学生成绩的方差
的值,且分别求出甲,乙两组学生成绩的方差 ,并根据结果判断那个组的数学成绩更好;
,并根据结果判断那个组的数学成绩更好;
(2)现要从测试成绩 分及以上的学生随机抽取
分及以上的学生随机抽取 名参加某次数学活动,求
名参加某次数学活动,求 名同学来自不同小组的概率.
名同学来自不同小组的概率.
已知函数 为常数)
为常数)
(1)求 的周期与
的周期与 ;
;
(2)当 时,求
时,求 的最值.
的最值.
若函数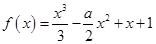 在区间
在区间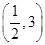 上有且只有一个极值点,则
上有且只有一个极值点,则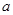 的取值范围为()
的取值范围为()
A.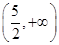 |
B.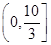 |
C.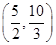 |
D.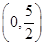 |
已知函数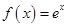
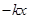 (
(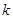 为常数)在点
为常数)在点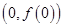 的切线与直线
的切线与直线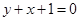 平行.
平行.
(1)求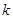 的值与函数
的值与函数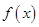 的单调区间;
的单调区间;
(2)证明:当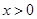 时,
时,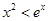
(3)证明:对任意给定的正数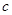 ,总存在
,总存在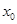 ,使得当
,使得当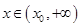 ,恒有
,恒有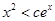 .
.