(本小题满分14分)
已知条件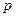 :
: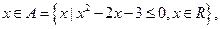
条件 :
: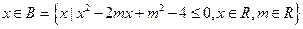
(Ⅰ)若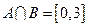 ,求实数
,求实数 的值;
的值;
(Ⅱ)若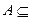
 ,求实数
,求实数 的取值范围.
的取值范围.
对于函数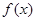 ,若存在x0∈R,使方程
,若存在x0∈R,使方程 成立,则称x0为
成立,则称x0为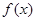 的不动点,已知函数
的不动点,已知函数 (a≠0).
(a≠0).
(1)当 时,求函数
时,求函数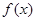 的不动点;
的不动点;
(2)若对任意实数b,函数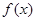 恒有两个相异的不动点,求a的取值范围;
恒有两个相异的不动点,求a的取值范围;
在经济学中,函数 的边际函数
的边际函数 定义为
定义为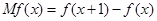 .某公司每月最多生产100台报警系统装置,生产
.某公司每月最多生产100台报警系统装置,生产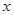 台(
台( )的收入函数为
)的收入函数为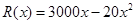 (单位:元),其成本函数为
(单位:元),其成本函数为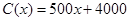 (单位:元),利润是收入与成本之差.
(单位:元),利润是收入与成本之差.
(1)求利润函数 及边际利润函数
及边际利润函数 的解析式,并指出它们的定义域;
的解析式,并指出它们的定义域;
(2)利润函数 与边际利润函数
与边际利润函数 是否具有相同的最大值?说明理由;
是否具有相同的最大值?说明理由;
已知函数
(1)求函数 的定义域;
的定义域;
(2)求函数 的零点;
的零点;
(3)若函数 的最小值为
的最小值为 ,求
,求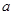 的值.
的值.
计算
(1)
(2)
已知全集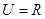 ,集合
,集合 ,
, ,
,
(1)求 .
.
(2)若集合 是集合A的子集,求实数k的取值范围.
是集合A的子集,求实数k的取值范围.