如图，四棱锥P—ABCD的底面是正方形，PA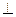
底面ABCD，PA=2，
，点E，F分别为棱AB，PD的中点。
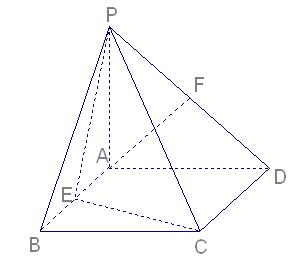
（1）在现有图形中，找出与AF平行的平面，并给出证明；
（2）判断平面PCE与平面PCD是否垂直？若垂直，给出证明；若不垂直，说明理由。
如图所示，为了制作一个圆柱形灯笼，先要制作4个全等的矩形骨架，总计耗用9.6米铁丝，再用S平方米塑料片制成圆柱的侧面和下底面(不安装上底面)．当圆柱底面半径r取何值时，S取得最大值？并求出该最大值(结果精确到0.01平方米)．
如图，在四边形ABCD中，∠DAB＝90°，∠ADC＝135°，AB＝5，CD＝2
，AD＝2，求四边形ABCD绕AD旋转一周所成几何体的表面积及体积．
如图，四棱锥P-ABCD中，PA⊥底面ABCD，AB⊥AD，点E在线段AD上，且CE∥AB.
(1)求证：CE⊥平面PAD；
(2)若PA＝AB＝1，AD＝3，CD＝
，∠CDA＝45°，求四棱锥P-ABCD的体积．
如图，底面边长为a，高为h的正三棱柱ABC-A1B1C1，其中D是AB的中点，E是BC的三等分点．求几何体BDEA1B1C1的体积．
四面体的六条棱中，有五条棱长都等于a.
(1)求该四面体的体积的最大值；
(2)当四面体的体积最大时，求其表面积．