已知函数 .
.
(Ⅰ)当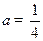 时,求函数
时,求函数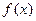 在
在 ,
, 上的最大值、最小值;
上的最大值、最小值;
(Ⅱ)令 ,若
,若 在
在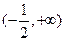 上单调递增,求实数
上单调递增,求实数 的取值范围.
的取值范围.
求值
(1)已知 ,
,
求 的值;
的值;
(2)已知 ,求
,求 的值。
的值。
在添加剂的搭配使用中,为了找到最佳的搭配方案,需要对各种不同的搭配方式作比较。在试制某种牙膏新品种时,需要选用两种不同的添加剂。现有芳香度分别为0,1,2,3,4,5的六种添加剂可供选用。根据试验设计原理,通常首先要随机选取两种不同的添加剂进行搭配试验。用 表示所选用的两种不同的添加剂的芳香度之和。
表示所选用的两种不同的添加剂的芳香度之和。
(Ⅰ)写出 的分布列;(以列表的形式给出结论,不必写计算过程)
的分布列;(以列表的形式给出结论,不必写计算过程)
(Ⅱ)求 的数学期望
的数学期望 。(要求写出计算过程或说明道理)
。(要求写出计算过程或说明道理)
(1)如果 展开式中,第四项与第六项的系数相等。求
展开式中,第四项与第六项的系数相等。求 ,并求展开式中的常数项;
,并求展开式中的常数项;
(2)求 展开式中的所有的有理项。
展开式中的所有的有理项。
已知函数 ,
, .(其中
.(其中 为自然对数的底数).
为自然对数的底数).
(1)设曲线 在
在 处的切线与直线
处的切线与直线 垂直,求
垂直,求 的值;
的值;
(2)若对于任意实数 ≥0,
≥0, 恒成立,试确定实数
恒成立,试确定实数 的取值范围;
的取值范围;
(3)当 时,是否存在实数
时,是否存在实数 ,使曲线C:
,使曲线C: 在点
在点 处的切线与
处的切线与 轴垂直?若存在,求出
轴垂直?若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
某连锁分店销售某种商品,每件商品的成本为4元,并且每件商品需向总店交 元(1≤a≤3)的管理费,预计当每件商品的售价为
元(1≤a≤3)的管理费,预计当每件商品的售价为 元(8≤x≤9)时,一年的销售量为(10-x)2万件.
元(8≤x≤9)时,一年的销售量为(10-x)2万件.
(1)求该连锁分店一年的利润L(万元)与每件商品的售价x的函数关系式L(x);
(2)当每件商品的售价为多少元时,该连锁分店一年的利润L最大,并求出L的最
大值M(a).