(本题10分)2010年9月起，长宁区为推进课程改革，落实“减负增效”，在部分学校六年级实施“阅读领航计划”试点研究.为了解在数学课堂内“阅读”指导对学生学习方法改进的程度，在社会实践阅读活动组织内容的受欢迎程度.在试点学校六年级随机抽取200名学生，对“学习方法改进”情况与“社会实践阅读活动组织内容”受欢迎程度两项作了调查.根据统计数据分别绘制成了下面扇形统计图与条形统计图．
(1)对“学生学习方法改进”程度的调查反馈中回答“显著改进”的学生有多少名？
(2)请将“社会实践阅读活动组织内容”受欢迎程度条形统计图补完整；
(3)若参加“社会实践阅读”试点学校的六年级学生约有1600名，根据上述统计数据，请你估计试点学校对“社会实践阅读活动组织内容”表示非常喜欢、喜欢及比较喜欢的学生共有多少名？
判断下列命题的真假，并说明理由．
（1）两个无理数的和仍然是无理数．
（2）如果a＞b，那么1﹣2a＜1﹣2b．
（1）化简：（a+2）（a﹣2）﹣a（a+1）；
（2）解不等式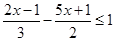
，并把它的解集在数轴上表示出来．
已知x=3是关于x的不等式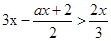
的解，求a的取值范围．
如下图所示，边长分别为a，b的两个正方形拼在一起，用代数式表示图中阴影部分的面积，并求a=8，b=5时，阴影部分的面积．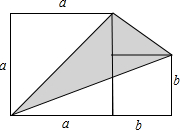
如图，△ABC中，∠C=90°，AC=3，BC=6，点P从A开始沿AC边向C点以1的速度移动，同时Q点从C沿边CB以2的速度向点B移动，设移动时间为t．请解答下列问题：
（1）出发几秒后，PQ=3？
（2）在运动过程中，线段PQ能否把△ABC面积平分？若能，求出t的值；若不能，请说明理由．