(本题满分12分,每小题满分各6分)如图(1),在△ABC和△EDC中,A C=CE=CB=CD,∠ACB=∠ECD=
C=CE=CB=CD,∠ACB=∠ECD= ,AB与CE交于F,ED与AB、BC分别交于M、H.
,AB与CE交于F,ED与AB、BC分别交于M、H.
(1)求证:CF=CH;
(2)如图(2),△ABC不动,将△EDC绕点C旋转到∠BCE= 时,试判断四边形AC
时,试判断四边形AC DM是什么四边形?并证明你的结论.
DM是什么四边形?并证明你的结论.
在边长为1的方格纸中建立直角坐标系,如图所示,O、A、B三点均为格点.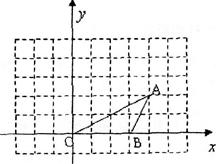
(1)直接写出线段OB的长;
(2)将△OAB绕点O沿逆时针方向旋转90°得到△OA′B′。请你画出△OA′B′,并求在旋转过程中,点B所经过的路径弧BB′的长度.
已知二次函数y=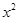 +bx+c的图象如图所示,它与x轴的一个交点的坐标为(-1,0),与y轴的交点坐标为(0,-3).
+bx+c的图象如图所示,它与x轴的一个交点的坐标为(-1,0),与y轴的交点坐标为(0,-3).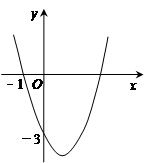
(1)求此二次函数的解析式;
(2)求此二次函数的图象与x轴的另一个交点的坐标;
(3)根据图象回答:当x取何值时,y<0?
如图是一个半圆形桥洞截面示意图,圆心为O,直径AB是河底线,弦CD是水位线,CD∥AB,且AB = 26m,OE⊥CD于点E.水位正常时测得OE∶CD=5∶24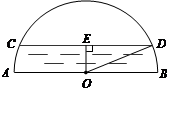
(1)求CD的长;
(2)现汛期来临,水面要以每小时4 m的速度上升,则经过多长时间桥洞会刚刚被灌满?
某商场销售一批名牌衬衣,平均每天可售出20件,每件衬衣盈利40元.为了扩大销售,
增加盈利,尽快减少库存,商场决定采取适当的降价措施.经调查发现,如果每件衬衣降价1元,商场平均
每天可多售出2件.
(1)若商场平均每天盈利1200元,每件衬衣应降价多少元?
(2)若要使商场平均每天的盈利最多,请你为商场设计降价方案.
如图,在△ABC中,∠C=90°, AD是∠BAC的平分线,O是AB上一点, 以OA为半径的⊙O经过点D。
(1)求证: BC是⊙O切线;
(2)若BD="5," DC="3," 求AC的长。