设椭圆的对称中心为坐标原点,其中一个顶点为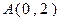 ,右焦点
,右焦点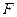 与点
与点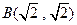 的距离为
的距离为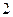 .
.
(1)求椭圆的方程;
(2)是否存在经过点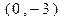 的直线
的直线 ,使直线
,使直线 与椭圆相交于不同的两点
与椭圆相交于不同的两点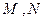 满足
满足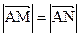 ?若存在,求出直线
?若存在,求出直线 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
(本小题满分12分)已知等差数列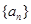 的公差大于0,且
的公差大于0,且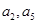 是方程
是方程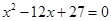 的两根,数列
的两根,数列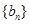 的前
的前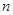 项的和为
项的和为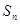 ,且
,且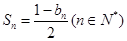 .
.
(1)求数列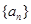 ,
,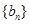 的通项公式;
的通项公式;
(2)若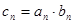 ,设数列
,设数列 的前
的前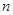 项和
项和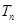 ,证明:
,证明: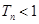 .
.
(本小题满分12分)如图1所示的梯形 中,
中, ,
, ,且
,且 ,如图2,沿
,如图2,沿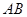 将四边形
将四边形 折起,使得面
折起,使得面 与面
与面 垂直,
垂直, 为
为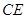 的中点.
的中点.
(1)求证: ;
;
(2)求二面角 的余弦值.
的余弦值.
(本小题满分12分)第53届世乒赛将于2015年4月26日至5月3日在中国苏州举办,中国女子乒乓球队队员经过顽强的拼搏冲入女子团体项目的决赛,已知团体赛采用“五局三胜”制,一、二、四、五场为单打,第三场为双打;一个队由三名运动员组成,每名运动员出场2次.根据历次大型比赛的统计,中国女队单打获胜的概率为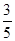 ,双打获胜的概率为
,双打获胜的概率为 .假如在决赛中的第一局,由于单打1号选手准备不够充分,中国女乒先输了第一场,在这个条件下.
.假如在决赛中的第一局,由于单打1号选手准备不够充分,中国女乒先输了第一场,在这个条件下.
(1)求中国女乒夺得团体冠军的概率;
(2)设决赛中比赛总的局数为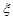 ,求
,求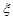 的分布列及
的分布列及 .(两问均用分数作答)
.(两问均用分数作答)
(本小题满分12分)已知函数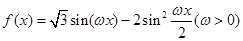 的最小正周期为
的最小正周期为 .
.
(1)若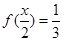 ,
,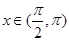 ,求
,求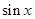 的值;
的值;
(2)已知 在
在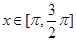 时恒成立,求实数
时恒成立,求实数 的取值范围.
的取值范围.
(本小题满分10分)已知数集A={a1,a2, ,an}(0≤a1<a2< <an,n≥2,n∈N*)具有性质P:"i,j(1≤i≤j≤n),
ai+aj与aj-ai两数中至少有一个属于A.
(1)分别判断数集{1,2,3,4}是否具有性质P,并说明理由;
(2)证明:a1=0;
(3)证明:当n=5时,a1,a2,a3,a4,a5成等差数列.