(满分12分)已知函数 ,常数
,常数 。
。
(1)若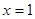 是函数
是函数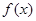 的一个极值点,求
的一个极值点,求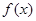 的单调区间;
的单调区间;
(2)若函数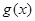
 在区间
在区间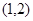 上是增函数,求
上是增函数,求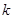 的取值范围;
的取值范围;
(3)设函数 ,求证:
,求证: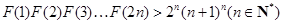
某商店统计了最近6个月某商品的进价x(元)与售价y(元)的对应数据如下表:
| x |
3 |
5 |
2 |
7 |
8 |
11 |
| y |
4 |
6 |
3 |
9 |
12 |
14 |
则回归直线方程是_______________.
注:线性回归直线方程系数公式:  ,a=y-bx
,a=y-bx
在直角坐标系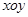 中,以O为圆心的圆与直线
中,以O为圆心的圆与直线 相切.
相切.
(1)求圆O的方程;
(2)圆O与 轴相交于
轴相交于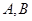 两点,圆内的动点
两点,圆内的动点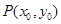 满足
满足 ,
,
求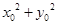 的取值范围.
的取值范围.
如图,四棱锥P -ABCD的底面是矩形,侧面PAD是正三角形,且侧面PAD⊥底面ABCD,E 为侧棱PD的中点。
(1)证明:PB//平面EAC;
(2)若AD="2AB=2," 求直线PB与平面ABCD所成角的正切值;
已知直线l经过点P(-2,5),且斜率为
(1)求直线l的方程;
(2)求与直线l切于点(2,2),圆心在直线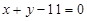 上的圆的方程.
上的圆的方程.
已知在⊿ABC中,A(3,2)、B(-1,5),C点在直线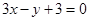 上,若⊿ABC的面积为10,求C点的坐标.
上,若⊿ABC的面积为10,求C点的坐标.