已知直线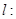
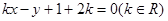．（1）证明：直线
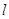过定点；（2）若直线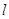不过第四象限，求
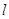的取值范围；（3）若直线交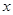
负半轴于点A，交
的正半轴于点B，O为坐标原点，设△ABC的面积为S，求S的最小值及此时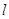的方程．
（本小题满分12分）
某赛季，甲、乙两名篮球运动员都参加了7场比赛，他们所有比赛得分的情况用如图所示的茎叶图表示．
（Ⅰ）求甲、乙两名运动员得分的中位数；
（Ⅱ）你认为哪位运动员的成绩更稳定？
（Ⅲ）如果从甲、乙两位运动员的7场得分中各随机抽取一场的得分，求甲的得分大于乙的得分的概率．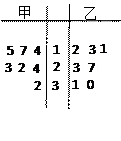
（本小题满分12分）
已知函数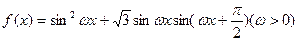
的最小正周期为
．
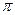（Ⅰ）求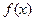
；
（Ⅱ）当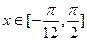
时，求函数
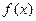的值域．
（本小题满分12分）
已知数列
（I）设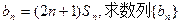
的通项公式；
（II）当
（本小题满分12分）
已知F1、F2分别是双曲线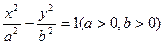
的左、右焦点，以坐标原点O为圆心，以双曲线的半焦距c为半径的圆与双曲线在第一象限的交点为A，与y轴正半轴的交点为B，点A在y轴上的射影为H，且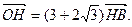
（I）求双曲线的离心率；
（II）若AF1交双曲线于点M，且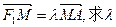
的值．
（本小题满分12分
）
已知函数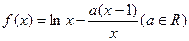
．
（I）求
的单调区间；
（II）求证：不等式
恒成立．