(本题16分)已知函数 ,其中e是自然数的底数,
,其中e是自然数的底数, ,
,
(1)当 时,解不等式
时,解不等式 ;
;
(2)若当 时,不等式
时,不等式 恒成立,求a的取值范围;
恒成立,求a的取值范围;
(3)当 时,试判断:是否存在整数k,使得方程
时,试判断:是否存在整数k,使得方程 在
在
上有解?若存在,请写出所有可能的k的值;若不存在,说明理由。
命题p:关于 的不等式
的不等式 对于一切
对于一切 恒成立,命题q:指数
恒成立,命题q:指数
函数 是增函数,若
是增函数,若 为真,
为真, 为假,求实数
为假,求实数 的取值范围;
的取值范围;
某企业生产甲、乙两种产品,已知生产每吨甲产品要用A原料3吨,B原料2吨;生产每吨乙产品要用A原料1吨,B原料3吨,销售每吨甲产品可获得利润5万元,每吨乙产品可获得利润3万元。该企业在一个生产周期内消耗A原料不超过13吨,B原料不超过18吨.那么在一个生产周期内该企业生产甲、乙两种产品各多少吨可获得最大利润,最大利润是多少?(用线性规划求解要画出规范的图形)
已知 为椭圆
为椭圆 的左、右焦点,
的左、右焦点, 是椭圆上一点。
是椭圆上一点。
(1)求 的最大值;
的最大值;
(2)若 且
且 的面积为
的面积为 ,求
,求 的值;
的值;
求与双曲线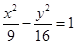 有共同渐近线,且过点(-3,
有共同渐近线,且过点(-3,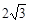 )的双曲线方程;
)的双曲线方程;
求过点P(3, 0)且与圆x2+6x+y2-91=0相内切的动圆圆心的轨迹方程。