. (本小题满分12分)
已知 函数
函数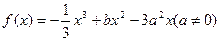 在
在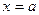 处取得极值.
处取得极值.
(Ⅰ) 求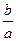 ;
;
(Ⅱ) 设函数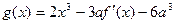 ,如果
,如果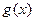 在开区间
在开区间 上存在极小值,求实数
上存在极小值,求实数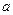 的取值范围.
的取值范围.
(本小题满分10分)
在平面直角坐标系 中,抛物线
中,抛物线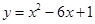 与坐标轴的交点都在圆
与坐标轴的交点都在圆 上.
上.
(1)求圆 的方程;
的方程;
(2)若线段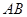 为圆
为圆 的直径,点
的直径,点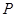 为直线
为直线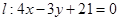 上的动点,求
上的动点,求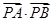 的最小值.
的最小值.
(本小题满分12分)
某工厂为了对新研发的一种产品进行合理定价,将对该产品按事先拟定的价格进行试销,得到如下数据:
| 单价x(元) |
8 |
8.2 |
8.4 |
8.6 |
8.8 |
9 |
| 销售y(件) |
90 |
84 |
83 |
80 |
75 |
68 |
(1)请根据上表提供的数据,用最小二乘法求出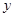 关于
关于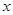 的线性回归方程
的线性回归方程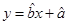 ;
;
其中(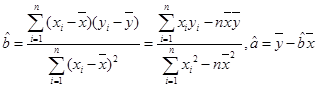 )
)
(2)预计在今后的销售中,销售与单价仍然服从(1)中的关系,且该产品的成本是4元/件,为使工厂获得最大利润,该产品的单价应定为多少元?(利润=销售收入-成本)
(本小题满分12分)
如图,四棱锥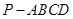 中,底面
中,底面 为平行四边形,
为平行四边形,
 ,
, 底面
底面 .
.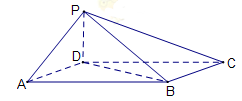
(1)证明: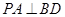 ;
;
(2)求三棱锥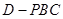 的高.
的高.
(本小题满分12分)
某校从参加高二年级期中考试的学生中随机抽取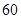 名学生,将其数学成绩(均为整数)分成六段
名学生,将其数学成绩(均为整数)分成六段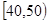 ,
,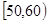 …
…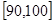 后得到如下部分频率分布直方图,观察图形的信息,回答下列问题:
后得到如下部分频率分布直方图,观察图形的信息,回答下列问题: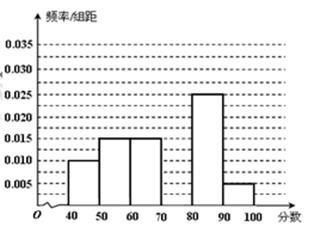
(1)求分数在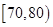 内的频率,并补全这个频率分布直方图;
内的频率,并补全这个频率分布直方图;
(2)根据频率分布直方图,估计本次数学成绩的平均数;
(3)用分层抽样的方法在分数段为 的学生中抽取一个容量为
的学生中抽取一个容量为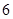 的样本,将该样本看成一个总体,从中任取
的样本,将该样本看成一个总体,从中任取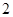 人,求至多有
人,求至多有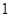 人分数在
人分数在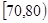 的概率.
的概率.
(本小题满分12分)
已知等比数列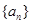 的前
的前 项和为
项和为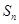 ,且
,且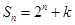 .
.
(1)求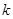 的值及数列
的值及数列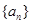 的通项公式
的通项公式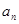 ;
;
(2)求数列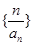 的前
的前 项和
项和 .
.