已知函数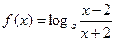 的定义域为[
的定义域为[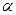 ,
,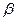 ],值域为
],值域为 ,
,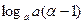 ],并且
],并且 在
在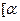 ,
, 上为减函数.
上为减函数.
(1)求 的取值范围;
的取值范围;
(2)求证: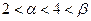 ;
;
(3)若函数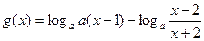 ,
, ,
, 的最大值为M,
的最大值为M,
求证: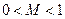
设函数f(x)=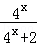 ,则:
,则:
(1)证明:f(x)+f(1﹣x)=1;
(2)计算:f( )+f(
)+f(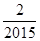 )+f(
)+f( )+…+f(
)+…+f(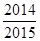 ).
).
(1)计算:
 +lg25+lg4+
+lg25+lg4+ +
+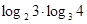 ;
;
(2)设集合A={x|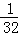 ≤2﹣x≤4},B={x|m﹣1<x<2m+1}.若A∪B=A,求m的取值范围.
≤2﹣x≤4},B={x|m﹣1<x<2m+1}.若A∪B=A,求m的取值范围.
设p:实数x满足x2-5ax+4a2<0(其中a>0),q:实数x满足2<x≤5
(1)若a=1,且p∧q为真,求实数x的取值范围;
(2)若 是
是 的必要不充分条件,求实数a的取值范围.
的必要不充分条件,求实数a的取值范围.
已知命题
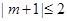 成立.命题
成立.命题 有实数根.若
有实数根.若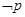 为假命题,
为假命题,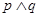 为假命题,求实数
为假命题,求实数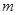 的取值范围.
的取值范围.
电影院为了解观看此部电影的观众年龄的情况,在某场次的100名观众中随机调查了20名观众,已知抽到的观众年龄可分成5组: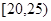 ,
,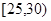 ,
,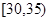 ,
, ,
,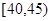 ,根据调查结果得出年龄情况残缺的频率分布直方图如下图所示。
,根据调查结果得出年龄情况残缺的频率分布直方图如下图所示。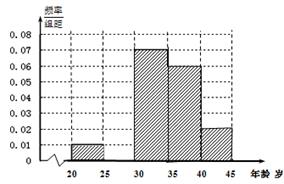
(1)根据已知条件,补充画完整频率分布直方图,并估计该电影院观看此部电影的观众年龄的平均数;
(2)现在从年龄属于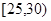 和
和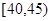 的两组中随机抽取2人,求他们属于同一年龄组的概率。
的两组中随机抽取2人,求他们属于同一年龄组的概率。