(1)计算:
 +lg25+lg4+
+lg25+lg4+ +
+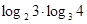 ;
;
(2)设集合A={x|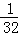 ≤2﹣x≤4},B={x|m﹣1<x<2m+1}.若A∪B=A,求m的取值范围.
≤2﹣x≤4},B={x|m﹣1<x<2m+1}.若A∪B=A,求m的取值范围.
.甲、乙两同学利用暑假到某县进行社会实践,对该县的养鸡场连续六年来的规模进行调查研究,得到如下两个不同的信息图.(A)图表明:从第1年平均每个养鸡场出产1万只鸡上升到第6年平均每个养鸡场出产2万只鸡;(B)图表明:由第1年养鸡场个数30个减少到第6年的10个.
请你根据提供的信息解答下列问题:
(1)第二年的养鸡场的个数及全县出产鸡的总只数各是多少?
(2)哪一年的规模最大?为什么?
已知数列{an}是等差数列,bn= ,b1+b2+b3=
,b1+b2+b3= ,b1b2b3=
,b1b2b3= ,求an.
,求an.
首项为a1,公差为d的整数等差数列{an}满足下列两个条件:(1)a3+a5+a7=93;(2)满足an>100的n的最小值是15.试求公差d和首项a1的值.
比较大小:
(1)log0.27和log0.29;(2)log35和log65;
(3)(lgm)1.9和(lgm)2.1(m>1);(4)log85和lg4.
设函数f(x)=x2-x+b,且f(log2a)=b,log2[f(a)]=2(a≠1),求f(log2x)的最小值及对应的x的值.