(本大题满分12分)某校高三年级一次数学考试后,为了解学生的数学学习情况,随机抽取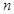 名学生的数学成绩,制成表所示的频率分布表.
名学生的数学成绩,制成表所示的频率分布表.
| 组号 |
分组 |
频数 |
频率 |
| 第一组 |
 |
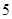 |
 |
| 第二组 |
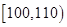 |
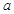 |
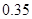 |
| 第三组 |
 |
 |
 |
| 第四组 |
 |
 |
 |
| 第五组 |
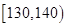 |
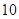 |
 |
| 合计 |
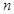 |
 |
|
(1)求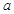 、
、 、
、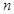 的值;
的值;
(2)若从第三、四、五组中用分层抽样方法抽取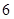 名学生,并在这
名学生,并在这 名学生中随机抽取
名学生中随机抽取 名学生与张老师面谈,求第三组中至少有
名学生与张老师面谈,求第三组中至少有 名学生与张老师面谈的概率
名学生与张老师面谈的概率
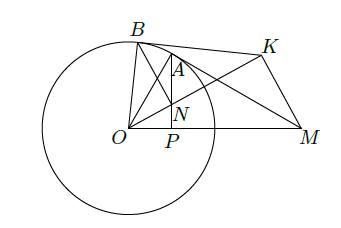
如图所示,过圆
外一点
作它的一条切线,切点为
,过
点作直线
垂直于直线
,垂足为
. 
(1)证明:
;
(2)
为线段
上一点,直线
垂直于直线
,且交圆
于
点.过点
的切线交直线
于
.证明:
.
如图所示,△ABC是⊙O的内接三角形,且AB=AC,AP是∠BAC的外角的平分线,弦CE的延长线交AP于点D.求证:AD2=DE·DC.
已知:如图所示,从Rt△ABC的两直角边AB,AC向外作正方形ABFG及ACDE,CF,BD分别交AB,AC于P,Q.求证:AP=AQ.
如图所示,AB是⊙O的直径,G为AB延长线上的一点,GCD是⊙O的割线,过点G作AB的垂线,交AC的延长线于点E,交AD的延长线于点F,过G作⊙O的切线,切
点为H.求证:(1)C,D,F,E四点共圆;
(2)GH2=GE·GF.
自圆O外一点P引切线与圆切于点A,M为PA的中点,过M引割线交圆于B,C两点.求证:∠MCP=∠MPB.