(11分)如图,抛物线 经过
经过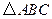 的三个点,已知
的三个点,已知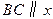 轴,点
轴,点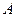 在
在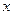 轴上,点
轴上,点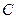 在
在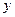 轴上,且
轴上,且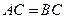 .
.
(1)求抛物线的对称轴;
(2)写出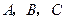 三点的坐标并求抛物线的解析式;
三点的坐标并求抛物线的解析式;
(3)探究:若点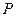 是抛物线对称轴上且在
是抛物线对称轴上且在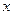 轴下方的动点,是否存在
轴下方的动点,是否存在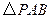 是等腰三角形?若存在,请在图中画出所有符合条件的P点,然后直接写出点
是等腰三角形?若存在,请在图中画出所有符合条件的P点,然后直接写出点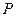 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.

《中华人民共和国道路交通安全法》规定:小汽车在城市道路上行驶速度不得超过70km/h.如图,一辆小汽车在一条城市道路上直道行驶,某一时刻刚好行驶到路对面车速检测仪(点A)的正前方30m处(点C),过了2s后,测得小汽车与车速检测仪间的距离AB为50m.这辆小汽车超速了吗?
如图是用硬纸板做成的四个全等的直角三角形(两直角边长分别是a、b,斜边长为c)和一个正方形(边长为c).请你将它们拼成一个能验证勾股定理的图形.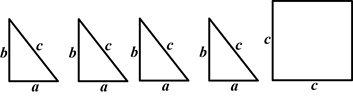
(1)画出拼成的这个图形的示意图;
(2)用(1)中画出的图形验证勾股定理.
在Rt△ABC中,∠C=90°,AC=8,BC=6,CD⊥AB,垂足为D,求DB的长.
如图,在△ABC中,AD⊥BC,垂足为D,∠B=60°,∠C=45°.
(1)求∠BAC的度数;
(2)若AC=2,求AD的长.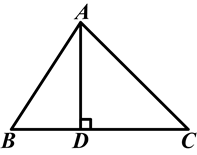
阅读材料:
小明在学习了二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如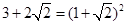 .善于思考的小明进行了以下探索:
.善于思考的小明进行了以下探索:
设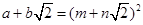 (其中a、b、m、n均为正整数),则有
(其中a、b、m、n均为正整数),则有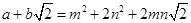 ,
,
∴a=m2+2n2,b=2mn.
这样小明就找到了一种把类似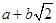 的式子化为平方式的方法.
的式子化为平方式的方法.
请你仿照小明的方法探索并解决下列问题:
(1)当a、b、m、n均为正整数时,若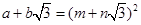 ,用含m、n的式子分别表示a、b,得a=________,b=________;
,用含m、n的式子分别表示a、b,得a=________,b=________;
(2)利用所探索的结论,找一组正整数a、b、m、n填空: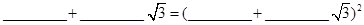 ;
;
(3)若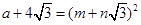 ,且a、m、n均为正整数,求a的值.
,且a、m、n均为正整数,求a的值.