(本题满分10分,第(1)(2)小题满分各3分,第(3)小题满分4分)
国家教育部规定“中小学生每天在校体育活动时间不低于1小时”.2011年,为了了解我市毕业班学生体育活动情况,随机对我市240名毕业班学生进行调查,调查内容为:
第一问 你平均每天在校参加体育活动的时间是多少?
A.超过1小时 B.0.5~1小时 C.低于0.5小时
如果第一问没有选A,请继续回答第二问
第二问 在校参加体育活动的时间没有超过1小时的原因是什么?
A.不喜欢 B.没时间 C.其他
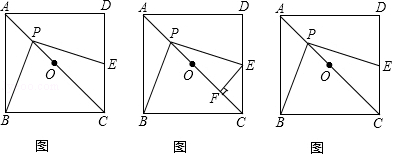
以下是根据所得的数据制成的统计图的一部分.
根据以上信息,解答下列问题:
(1)每天在校锻炼时间超过1小时的人数是 ;
(2)请将条形图补充完整;
(3)2011年我市初中毕业生约为8.4万人,请你估计今年全市初中毕业生中每天锻炼时间低于0.5小时的学生约有 万人.
一个不透明的口袋中装有4个球,分别是红球和白球,这些球除颜色外都相同,将球搅匀,先从中任意摸出一个球,恰好摸到红球的概率等于 .
(1)求口袋中有几个红球?
(2)先从中任意摸出一个球,从余下的球中再摸出一个球,请用列表法或树状图法求两次摸到的球中一个是红球和一个是白球的概率.
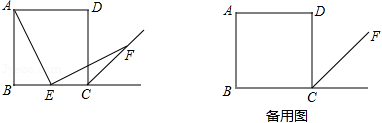
如图,四边形 ABCD是正方形,点 E是 BC的中点,∠ AEF=90°, EF交正方形外角的平分线 CF于 F.求证: AE= EF.
在我市十个全覆盖工作的推动下,某乡镇准备在相距3千米的 A、 B两个工厂间修一条笔直的公路,在工厂 A北偏东60°方向、工厂北偏西45°方向有一点 P,以 P点为圆心,1.2千米为半径的区域是一个村庄,问修筑公路时,这个村庄是否有居民需要搬迁?(参考数据: , )

如图,在平面直角坐标系内,抛物线 y=﹣ x 2+ bx+ c与 x轴交于 A, B两点( A在 B的左侧),与 y轴交于点 C,且 A, B两点的横坐标分别是方程 x 2﹣2 x﹣3=0的两个实数根.
(1)求抛物线的解析式.
(2)若抛物线的顶点为 M,作点 M关于 x轴的对称点 N,顺次连接 A, M, B, N,在抛物线上存在点 D,使直线 CD将四边形 AMBN分成面积相等的两个四边形,求点 D的坐标.
(3)在抛物线上是否存在点 P,使△ PBC中 BC边上的高为 ?若存在,请直接写出满足条件的所有 P点的坐标;若不存在,请说明理由.
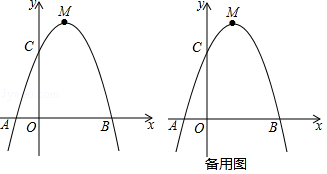
如图①,正方形 ABCD中,点 O是对角线 AC的中点,点 P是线段 AO上(不与 A, O重合)的一个动点,过点 P作 PE⊥ PB且 PE交边 CD于点 E.
(1)求证: PB= PE.
(2)如图②,若正方形 ABCD的边长为2,过 E作 EF⊥ AC于点 F,在 P点运动的过程中, PF的长度是否发生变化?若不变,试求出这个不变的值;若变化,请说明理由.
(3)如图③,用等式表示线段 PC, PA, CE之间的数量关系.