(本小题满分12分)求通过原点且与两直线l1:x+2y-9=0,l2:2x-y+2=0相切的圆的方程
(本小题满分12分)某厂家根据以往的经验得到有关生产销售规律如下:每生产 (百台),其总成本为
(百台),其总成本为 (万元),其中固定成本2万元,每生产1百台需生产成本1万元(总成本
(万元),其中固定成本2万元,每生产1百台需生产成本1万元(总成本 固定成本
固定成本 生产成本);销售收入
生产成本);销售收入 (万元)满足:
(万元)满足: (Ⅰ)要使工厂有盈利,求
(Ⅰ)要使工厂有盈利,求 的取值范围;
的取值范围;
(Ⅱ)求生产多少台时,盈利最多?
(本小题满分16分)设实数a为正数,函数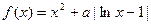 .(Ⅰ)当
.(Ⅰ)当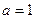 时,求曲线
时,求曲线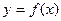 在
在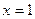 处的切线方程; (Ⅱ)当
处的切线方程; (Ⅱ)当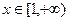 时,求函数
时,求函数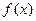 的最小值.
的最小值.
(本小题满分16分)已知数列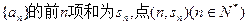 在函数
在函数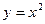 的图象上,数列
的图象上,数列 满足
满足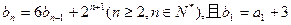 (1)求数列
(1)求数列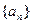 的通项公式;(2)证明列数
的通项公式;(2)证明列数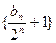 是等比数列,并求数列
是等比数列,并求数列 的通项公式;(3)设数列
的通项公式;(3)设数列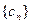 满足对任意的
满足对任意的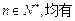
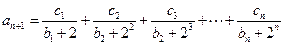 成立,
成立,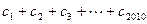 的值。
的值。
(本小题满分15分)某生产旅游纪念品的工厂,拟在2010年度将进行系列促销活动.经市场调查和测算,该纪念品的年销售量x万件与年促销费用t万元之间满足3-x与t+1成反比例.若不搞促销活动,纪念品的年销售量只有1万件.已知工厂2010年生产纪念品的固定投资为3万元,每生产1万件纪念品另外需要投资32万元.当工厂把每件纪念品的售价定为:“年平均每件生产成本的150%”与“年平均每 件所占促销费一半”之和时,则当年的产量和销量相等.(利润=收入-生产成本-促销费用)(1)求出x与t所满足的关系式;(2)请把该工厂2010年的年利润y万元表示成促销费t万元的函数;(3)试问:当2010年的促销费投入多少万元时,该工厂的年利润最大?
件所占促销费一半”之和时,则当年的产量和销量相等.(利润=收入-生产成本-促销费用)(1)求出x与t所满足的关系式;(2)请把该工厂2010年的年利润y万元表示成促销费t万元的函数;(3)试问:当2010年的促销费投入多少万元时,该工厂的年利润最大?
(本小题满分14分)如图,在正方体 中,
中, 、
、 分别
分别
为棱 、
、 的中点.(1)求证:
的中点.(1)求证: ∥平面
∥平面 ;
;
(2)求证:平面 ⊥平面
⊥平面 ;
;
(3)如果 ,一个动点从点
,一个动点从点 出发在正方体的
出发在正方体的
表面上依次经过棱 、
、 、
、 、
、 、
、 上的点,
上的点,
最终又回到点 ,指出整个路线长度的最小值并说明理由.
,指出整个路线长度的最小值并说明理由.