(本小题满分12分)
已知函数 .
.
(1)求 的极值;
的极值;
(2)若 在
在 上恒成立,求
上恒成立,求 的取值范围;
的取值范围;
(3)已知 ,且
,且 ,求证:
,求证: .
.
(本小题满分12分)如图所示,已知在四棱锥 中,
中,  ∥
∥ ,
, ,
,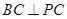 ,
,
且

(1)求证: 平面
平面 ;
;
(2)试在线段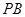 上找一点
上找一点 ,使
,使 ∥平面
∥平面 , 并说明理由;
, 并说明理由;
(3)若点 是由(2)中确定的,且
是由(2)中确定的,且 ,求四面体
,求四面体 的体积.
的体积.
(本小题满分12分)已知数列 是等比数列,首项
是等比数列,首项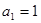 ,公比
,公比 ,其前
,其前 项和为
项和为 ,且
,且 ,
, ,
, 成等差数列.
成等差数列.
(1)求数列 的通项公式;
的通项公式;
(2)若数列 满足
满足 ,
, 为数列
为数列 的前
的前 项和,若
项和,若 恒成立,求
恒成立,求 的最大值.
的最大值.
(本小题满分12分)某厂家生产甲、乙、丙三种样式的杯子,每种杯子均有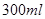 和
和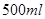 两种型号,某月的产量(单位:个)如下表所示:
两种型号,某月的产量(单位:个)如下表所示:
| 型号 |
甲样式 |
乙样式 |
丙样式 |
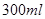 |
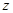 |
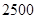 |
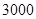 |
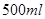 |
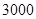 |
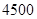 |
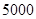 |
按样式用分层抽样的方法在这个月生产的杯子中随机的抽取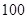 个,其中有乙样式的杯子
个,其中有乙样式的杯子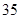 个.
个.
(1)求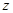 的值;
的值;
(2)用分层抽样的方法在甲样式的杯子中抽取一个容量为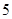 的样本,从这个样本中任取
的样本,从这个样本中任取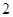 个杯子,求至少有
个杯子,求至少有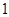 个
个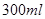 的杯子的概率.
的杯子的概率.
(本小题满分12分)在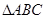 中,
中,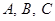 所对的边分别
所对的边分别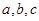 ,
,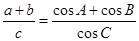 ,
,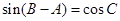 .
.
(1)求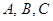 ;
;
(2)若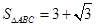 ,求
,求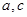 .
.
(本小题满分14分)在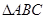 中,
中, 的坐标分别是
的坐标分别是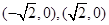 ,点
,点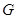 是
是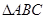 的重心,
的重心,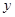 轴上一点
轴上一点 满足
满足 ,且
,且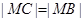 .
.
(1)求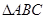 的顶点
的顶点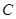 的轨迹
的轨迹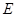 的方程;
的方程;
(2)直线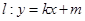 与轨迹
与轨迹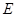 相交于
相交于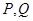 两点,若在轨迹
两点,若在轨迹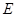 上存在点
上存在点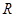 ,使四边形
,使四边形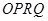 为平行四边形(其中
为平行四边形(其中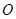 为坐标原点),求
为坐标原点),求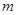 的取值范围.
的取值范围.