(本小题满分12分)已知函数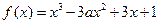 .
.
(1)设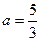 ,求函数
,求函数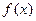 在
在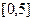 上的最大值和最小值;
上的最大值和最小值;
(2)设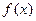 在区间
在区间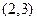 中至少有一个极值点,求
中至少有一个极值点,求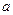 的取值范围.
的取值范围.
已知两曲线参数方程分别为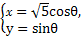 (0≤θ<π)和
(0≤θ<π)和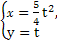 (t∈R),求它们的交点坐标.
(t∈R),求它们的交点坐标.
设直线l1的参数方程为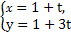 (t为参数),直线l2的方程为y=3x+4,求l1与l2间的距离.
(t为参数),直线l2的方程为y=3x+4,求l1与l2间的距离.
在直角坐标系xOy中,以O为极点,x轴非负半轴为极轴建立极坐标系,曲线C的极坐标方程为ρcos(θ-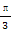 )=1,M,N分别为C与x轴,y轴的交点.
)=1,M,N分别为C与x轴,y轴的交点.
(1)写出C的直角坐标方程,并求M,N的极坐标.
(2)设MN的中点为P,求直线OP的极坐标方程.
在极坐标系下,已知圆O:ρ=cosθ+sinθ和直线l:ρsin(θ-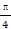 )=
)=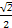 .
.
(1)求圆O和直线l的直角坐标方程.
(2)当θ∈(0,π)时,求直线l与圆O公共点的一个极坐标.
已知圆O1和圆O2的极坐标方程分别为ρ=2,ρ2-2 ρcos(θ-
ρcos(θ- )=2.
)=2.
(1)把圆O1和圆O2的极坐标方程化为直角坐标方程.
(2)求经过两圆交点的直线的极坐标方程.