（本小题满分7分）已知：关于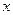
的一元二次方程
．
（1）若方程有两个不相等的实数根，求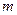
的取值范围；
（2）在（1）的条件下，求证：无论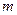取何值，抛物线y=
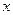总过轴上的一个固定点；
（3）若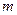为正整数，且关于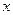的一元二次方程有两个不相等的整数根，把抛物线y=向右平移4个单位长度，求平移后的抛物线的解析式．
已知：如图，在△ABC中，BC＝AC，以BC为直径的⊙O与边AB相交于点D，DE⊥AC，垂足为点E.
(1)求证：点D是AB的中点；
(2)判断DE与⊙O的位置关系，并证明你的结论；
(3)若⊙O的直径为18，cosB＝
，求DE的长．
某地菜农张三收获了大白菜20吨，辣椒12吨．现计划租用甲、乙两种货车共8辆将这批蔬菜全部运往外地销售；已知一辆甲种货车可装大白菜4吨和辣椒1吨，一辆乙种货车可装大白菜和辣椒各2吨．
(1)请问张三有几种方案安排甲、乙两种货车可一次性地将水果运到销售地？
(2)若甲种货车每辆要付运输费300元，乙种货车每辆要付运输费240元，则菜农张三应选择哪种方案，使运输费最少？最少运费是多少？
如图，平行于y轴的直尺（一部分）与双曲线
（x＞0）交于点A、C，与x轴交于点B、D，连结AC．点A、B的刻度分别为5、2（单位：cm），直尺的宽度为2cm，OB=2 cm．
(1)求k的值；
(2)求经过A、C两点的直线解析式.
有4张形状、大小和质地都相同的卡片，正面分别写有字母A、B、C、D和一个算式，背面完全一致．如图所示，将这4张卡片背面向上洗匀，从中随机抽取1张，不放回，接着再随机抽取1张．
（1）请用画树形图或列表法表示出所有的可能结果；（卡片可用A、B、C、D表示）
（2）将“第一张卡片上的算式是正确，同时第二张卡片上的算式是错误”记为事件A，求事件A的概率．
如图，在平行四边形ABCD中，E、F为BC上两点，且BE=CF,AF=DE. 
（1）找出图中一对全等的三角形，并证明；
（2）求证：四边形ABCD是矩形．