(本小题满分14分)已知 ,若函数
,若函数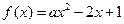 在区间
在区间 上
上
的最大值为 ,最小值为
,最小值为 ,令
,令 .
.
(1)求 的函数表达式;
的函数表达式;
(2)判断函数 在区间
在区间 上的单调性,并求出
上的单调性,并求出 的最小值.
的最小值.
△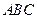 中,内角
中,内角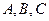 的对边分别为
的对边分别为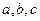 ,已知
,已知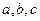 成等比数列,
成等比数列,
求(1) 的值;(2)设
的值;(2)设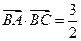 ,求
,求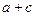 的值.
的值.
抛物线x2=4y的焦点为F,过点(0,-1)作直线l交抛物线A、B两点,再以AF、BF为邻边作平行四边形FABR,试求动点R的轨迹方程.
已知抛物线y2=4ax(0<a<1)的焦点为F,以A(a+4,0)为圆心,|AF|为半径在x轴上方作半圆交抛物线于不同的两点M和N,设P为线段MN的中点,
(Ⅰ)求|MF|+|NF|的值;
(Ⅱ)是否存在这样的a值,使|MF|、|PF|、|NF|成等差数列?如存在,求出a的值,
已知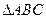 中,
中, ,则
,则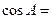
A.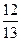 |
B.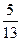 |
C. |
D.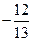 |
已知不等式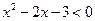 的解集为A,不等式
的解集为A,不等式 的解集为B,
的解集为B,
(1)求A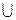 B
B
(2)若不等式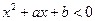 的解集是A
的解集是A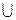 B,求
B,求 的解集。
的解集。