(本小题满分12分)如图甲,在平面四边形ABCD中,已知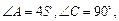
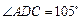 ,
, ,现将四边形ABCD沿BD折起,使
,现将四边形ABCD沿BD折起,使 平面ABD
平面ABD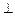
平面BDC(如图乙),设点E、F分别为棱AC、AD的中点.
(Ⅰ)求证:DC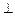 平面ABC;
平面ABC;
(Ⅱ)设 ,求三棱锥A-BFE的体积.
,求三棱锥A-BFE的体积.
设数列 的前
的前 项和为
项和为 ,满足
,满足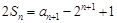 ,
,
 ,且
,且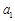 ,
,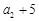 ,
,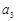 成等差数列.
成等差数列.
(1)求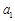 ,
, 的值;
的值;
(2) 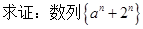 是等比数列
是等比数列
(3)证明:对一切正整数 ,有
,有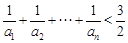 .
.
已知 .
.
(1)求函数 在
在 上的最小值;
上的最小值;
(2)对一切 恒成立,求实数
恒成立,求实数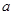 的取值范围;
的取值范围;
(3)证明:对一切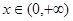 ,都有
,都有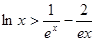 成立.
成立.
已知函数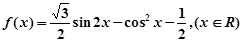
(1)当 时,求函数
时,求函数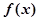 的最小值和最大值;
的最小值和最大值;
(2)设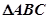 的内角
的内角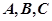 的对应边分别为
的对应边分别为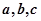 ,且
,且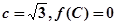 ,若向量
,若向量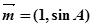 与向量
与向量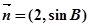 共线,求
共线,求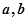 的值.
的值.
本着健康、低碳的生活理念,租自行车骑游的人越来越多。某自行车租车点的收费标准是每车每次租车时间不超过两小时免费,超过两小时的部分每小时收费标准为2元(不足1小时的部分按1小时计算)。有甲乙两人相互独立来该租车点租车骑游(各租一车一次),设甲、乙不超过两小时还车的概率分别为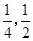 ;两小时以上且不超过三小时还车的概率分别为
;两小时以上且不超过三小时还车的概率分别为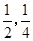 ;两人租车时间都不会超过四小时。
;两人租车时间都不会超过四小时。
(1)求出甲、乙两人所付租车费用相同的概率;
(2)设甲、乙两人所付的租车费用之和为随机变量 ,求
,求 的分布列与数学期望
的分布列与数学期望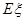
已知向量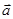 =(cos
=(cos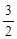 x,sin
x,sin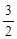 x),
x), 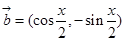 ,且x∈[0,
,且x∈[0,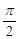 ].
].
(1)求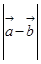
(2)设函数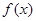 =
=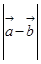 +
+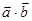 ,求函数
,求函数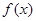 的最值及相应的
的最值及相应的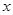 的值。
的值。