设函数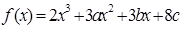
在
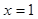及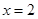
时取得极值．
（1）求a、b的值；
（2）当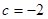
时，求函数
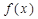在区间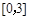
上的最大值．
袋中有同样的球5个，其中3个红色，2个黄色，现从中随机且不返回地摸球，每次摸1个，当两种颜色的球都被摸到时，即停止摸球，记随机变量
为此时已摸球的次数，求：
(1)随机变量的概率分布；
(2)随机变量的数学期望.
(1)已知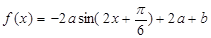
，
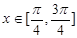，是否存在常数
时，使得
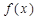的值域为[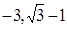
]？若存在，求出
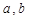的值，若不存在，说明理由。
(2)若关于
的方程
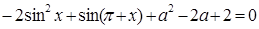在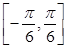
内有实数根，求实数
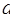的范围。
圆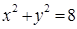
内有一点
，
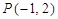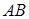为过点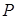
且倾斜角为
的弦，
（1）当＝135０时，求
;
（2）当弦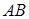被点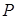平分时，求出直线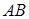的方程;
（3）设过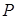点的弦的中点为
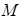，求点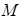的轨迹方程.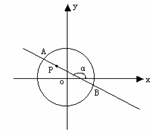 
如图，在平面直角坐标系中，锐角
和钝角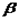
的终边分别与单位圆交于
，
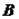两点．
（1）如果
、
两点的纵坐标分别为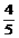
、
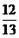，求
和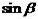
；
（2）在（1）的条件下，求
的值；
（3）已知点
，求函数f（
）=
的值域．
满足：
的前项和为
及
；
，求数列
的前项和